
 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源:2017-2018学年内蒙古赤峰市七年级(上)期中数学试卷 题型:单选题
在数轴上表示a、b两数的点如图所示,则下列判断正确的是( )
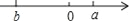
A. a+b>0 B. a+b<0 C. a>|b| D. |a|>|b|
B 【解析】试题解析:∵b<0<a,而且a<|b|, ∴a+b<0, ∴选项A不正确,选项B正确; ∵a<|b|, ∴选项C不正确; ∵|a|<|b|, ∴选项D不正确. 故选B.查看答案和解析>>
科目:初中数学 来源:福建省南平市2018届九年级上学期第二次月考数学试卷 题型:单选题
同圆的内接正三角形与内接正方形的边长的比是( )
A. 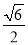 B.
B. 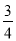 C.
C. 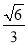 D.
D. 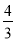
查看答案和解析>>
科目:初中数学 来源:贵州铜仁伟才学校2017-2018学年八年级上学期期中考试数学试卷 题型:解答题
随着柴静纪录片《穹顶之下》的播出,全社会对空气污染问题越来越重视,空气净化器的销量也大增,商社电器从厂家购进了A,B两种型号的空气净化器,已知一台A型空气净化器的进价比一台B型空气净化器的进价多300元,用7500元购进A型空气净化器和用6000元购进B型空气净化器的台数相同.
(1)求一台A型空气净化器和一台B型空气净化器的进价各为多少元?
(2)在销售过程中,A型空气净化器因为净化能力强,噪音小而更受消费者的欢迎.为了增大B型空气净化器的销量,商社电器决定对B型空气净化器进行降价销售,经市场调查,当B型空气净化器的售价为1800元时,每天可卖出4台,在此基础上,售价每降低50元,每天将多售出1台,如果每天商社电器销售B型空气净化器的利润为3200元,请问商社电器应将B型空气净化器的售价定为多少元?
(1)每台B型空气净化器、每台A型空气净化器的进价分别为1200元,1500元; (2)应将B型空气净化器的售价定为1600元. 【解析】试题分析:(1)设每台B种空气净化器为x元,A种净化器为(x+300)元,根据用6000元购进B种空气净化器的数量与用7500元购进A种空气净化器的数量相同,列方程求解; (2)根据总利润=单件利润×销量列出一元二次方程求解即可. 试题解...查看答案和解析>>
科目:初中数学 来源:贵州铜仁伟才学校2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
我们把分子为1的分数叫做理想分数,如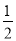 ,
, 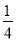 ,…,任何一个理想分数都可以写成两个不同理想分数的和,如
,…,任何一个理想分数都可以写成两个不同理想分数的和,如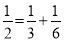 ;
; 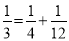 ;
; 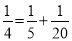 ;
; 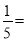 ______________;根据对上述式子的观察,请你思考:如果理想分数
______________;根据对上述式子的观察,请你思考:如果理想分数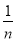 (n是不小于2的整数)
(n是不小于2的整数)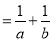 ,那么
,那么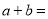 ________________.(用含n的式子表示).
________________.(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源:贵州铜仁伟才学校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
下列语句:
①“反证法”就是举反例说明一个命题是假命题;②“等腰三角形两底角相等”的逆命题是真命题;③分式有意义的条件是分子为零且分母不为零;④同旁内角互补.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
A 【解析】试题解析:①“反证法”就是从反面的角度思考问题的证明方法,故错误; ②“等腰三角形两底角相等”的逆命题是有两个角相等的三角形为等腰三角形,是真命题,正确; ③分式有意义的条件是分母不为零,故错误; ④两直线平行,同旁内角互补.故错误. 正确的有1个. 故选A查看答案和解析>>
科目:初中数学 来源:贵州铜仁伟才学校2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
计算(π-3)0的结果为()
A. 0.14 B. 1 C. π D. 0
B 【解析】∵任何非0实数的0次幂都为1,即, ∴B正确. 故选B.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市鄞州区2017-2018学年九年级上册数学第一次月考试卷 题型:单选题
下列每张方格纸上都有一个三角形,只用圆规就能做出三角形的外接圆的是( )
 ①
①  ②
②  ③
③  ④
④
A. ①② B. ①③ C. ②④ D. ③④
C 【解析】根据三角形外接圆的性质可知图②和图④只能用圆规就能做出三角形的外接圆, 故选:C.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市鄞州区九校2017-2018学年八年级上册数学第一次月考试卷 题型:填空题
如图,在△ABC中,D是BC上一点,AC=AD=DB,∠BAC=102°,则∠ADC=_____.
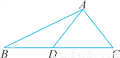
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com