
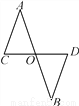
完成下面的证明:
如图,AB和CD相交于点O,∠C=∠COA,∠D=∠BOD.
求证:∠A=∠B.
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源:云南省2016-2017学年七年级上学期期末考试数学试卷 题型:填空题
比较大小:-2_______ -3(填“>”、“<” 或 “=”号).
> 【解析】∵|-2|=2,|-3|=3,2<3, ∴-2>-3, 故答案为:>.查看答案和解析>>
科目:初中数学 来源:辽宁省葫芦岛市建昌县2017-2018学年八年级上学期期末测评数学试卷 题型:解答题
观察下列等式:① 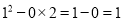 ;②
;②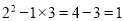 ;
;
③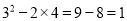 ;④
;④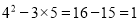 .
.
(1)请你按着这个规律写出第五个和第六个等式: , .
(2)把这个规律用含字母n(n是不小于l的正整数)的式子表示出来.
(1), ;(2). 【解析】试题分析:(1)根据①②③④的算式中,变与不变的部分,找出规律,写出新的算式; (2)将(1)中,发现的规律,由特殊到一般,得出结论. 试题解析:(1), ; (2).查看答案和解析>>
科目:初中数学 来源:辽宁省葫芦岛市建昌县2017-2018学年八年级上学期期末测评数学试卷 题型:单选题
下列方程是分式方程的是( )
A. 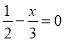 B.
B. 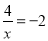 C.
C. 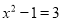 D. 2x+1=3x
D. 2x+1=3x
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(遵义):期中检测题 题型:解答题
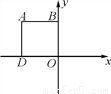
如图,已知正方形ABOD的周长为4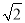 ,点P到x轴、y轴的距离与点A到x轴、y轴的距离分别相等.
,点P到x轴、y轴的距离与点A到x轴、y轴的距离分别相等.
(1)请你写出正方形ABOD各顶点的坐标;
(2)求点P的坐标及三角形PDO的面积.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(遵义):期中检测题 题型:填空题
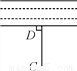
如图,从D处开渠引水到C处,则渠道CD最短,依据是__________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学下册(遵义):期中检测题 题型:单选题
下列语句:
①相等的角是对顶角;
②如果两条直线被第三条直线所截,那么同位角相等;
③过直线外一点有且只有一条直线与已知直线平行;
④平行线间的距离处处相等.
其中正确的命题是( )
A. ①② B. ②③ C. ③④ D. ①④
C 【解析】试题分析:根据对顶角的定义对①进行判断;根据平行线的性质对②进行判断;根据平行公理对③进行判断;根据平行线之间的距离对④进行判断. 【解析】 相等的角不一定是对顶角,所以①错误; 如果平行两条直线被第三条直线所截,那么同位角相等,所以②错误; 过直线外一点有且只有一条直线与已知直线平行,所以③正确; 平行线间的距离处处相等,所以④正确. 故选C. ...查看答案和解析>>
科目:初中数学 来源:2018年河南省驻马店市第一次中考模拟数学试卷 题型:填空题
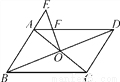
(2017·六盘水)如图,在?ABCD中,对角线AC,BD相交于点O,在BA的延长线上取一点E,连接OE交AD于点F.若CD=5,BC=8,AE=2,则AF=_______.
查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2018届九年级上学期期中考试数学试卷 题型:解答题
如图,在平面直角坐标系中.直线y=﹣x+3与x轴交于点B,与y轴交于点C,抛物线y=ax2+bx+c经过B,C两点,与x轴负半轴交于点A,连结AC,A(-1,0)
(1)求抛物线的解析式;
(2)点P(m,n)是抛物线上在第一象限内的一点,求四边形OCPB面积S关于m的函数表达式及S的最大值;
(3)若M为抛物线的顶点,点Q在直线BC上,点N在直线BM上,Q,M,N三点构成以MN为底边的等腰直角三角形,求点N的坐标.
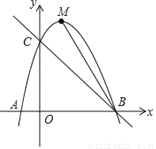
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com