练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知△ABC的三边长为a、b、c，满足a+b=10，ab=18，c=8，则此三角形为_____三角形．

    直角 【解析】根据已知：a+b=10，ab=18，c=8，可求（a+b）2﹣2ab=100﹣36=64，和c2=64，因此可得到a2+b2=c2，然后根据勾股定理可知此三角形是直角三角形． 故答案为：直角．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年海南省中考数学模拟试卷 题型：单选题

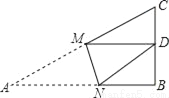
    如图，Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（　　）

    A. B. C. 4 D. 5

    C 【解析】试题分析：设BN=x，由折叠的性质可得DN=AN=9－x， ∵D是BC的中点， ∴BD=3， 在Rt△BDN中，x2+32=（9－x）2， 解得x=4． 故线段BN的长为4． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：山东省寿光市2017-2018学年七年级上期末模拟数学试卷 题型：解答题

    画出数轴，把下列各组数分别在数轴上表示出来，并按从大到小的顺序排列，用“＞”连接起来：

    　1，﹣2，3，﹣4，1.6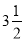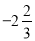， ， ，0．

    ＞3＞1.6＞1＞0＞﹣2＞﹣＞﹣4． 【解析】试题分析：先在数轴上表示出来，再根据右边的数总比左边的数大，即可得出答案． 试题解析：根据题意画图如下： 用“＞”连接起来：3＞3＞1.6＞1＞0＞﹣2＞﹣2＞﹣4．

    查看答案和解析>>

    科目：初中数学 来源：山东省寿光市2017-2018学年七年级上期末模拟数学试卷 题型：单选题

    下列结论中正确的是（　　）

    A. 在等式3a﹣b=3b+5的两边都除以3，可得等式a﹣2=b+5

    B. 如果2=﹣x，那么x=﹣2

    C. 在等式5=0.1x的两边都除以0.1，可得等式x=0.5

    D. 在等式7x=5x+3的两边都减去x﹣3，可得等式6x﹣3=4x+6

    B 【解析】选项A，在等式3a－6＝3b＋5的两边都除以3，可得等式a－2＝b＋ ，选项A错误；选项B， 如果2＝－x，那么x＝－2，根据移项法则可得选项B正确；选项C，在等式5＝0.1x的两边都除以0.1，可得等式x＝50，选项C错误；选项D，在等式7x＝5x＋3的两边都减去x－3，可得等式6x－3＝4x，选项D错误.故选B.

    查看答案和解析>>

    科目：初中数学 来源：2017年天津二十一中中考数学冲刺试卷（2） 题型：解答题

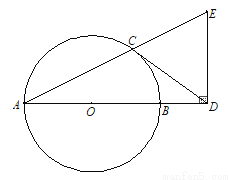
    如图，AB是⊙O的直径，CD与⊙O相切于点C，与AB的延长线交于点D，DE⊥AD且与AC的延长线交于点E.

    (1)求证：DC＝DE；

    (2)若tan∠CAB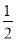＝，AB＝3，求BD的长.

    (1)证明见解析;(2)1. 【解析】试题分析：（1）利用切线的性质和等腰三角形的性质可以得出∠DCE=∠E，进而得出答案； （2）设BD=x，则AD=AB+BD=3+x，OD=OB+BD=1.5+x，利用勾股定理得出BD的长． 试题解析：（1）连接OC，∵CD是⊙O的切线，∴∠OCD=90°，∴∠ACO+∠DCE=90°，又∵ED⊥AD，∴∠EDA=90°，∴∠EAD+∠E=9...

    查看答案和解析>>

    科目：初中数学 来源：2017年天津二十一中中考数学冲刺试卷（2） 题型：单选题

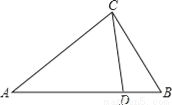
    如图，△ACD和△ABC相似需具备的条件是（　　）

    A. 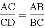B. 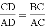C. AC2=AD•AB D. CD2=AD•BD

    C 【解析】试题分析：本题主要考查的就是三角形相似的判定，本题根据有一个角相等，且对应角的两边对应成比例，则两个三角形相似可以得出答案.根据题意可得∠A为公共角，则要使三角形相似则必须满足=. 点晴：本题主要考查的就是三角形相似的判定定理，在有一个角相等的情况下，必须是角的两边对应成比例，如果不是角的两边对应成比例，则这两个三角形不相似；相似还可以利用有两个角对应相等的两个三角形全等....

    查看答案和解析>>

    科目：初中数学 来源：2017年天津二十一中中考数学冲刺试卷（2） 题型：单选题

    6张如图1的长为a，宽为b（a＞b）的小长方形纸片，按图2方式不重叠地放在矩形ABCD内，未被覆盖的部分（两个矩形）用阴影表示．设左上角与右下角的阴影部分的面积的差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a，b满足（   ）

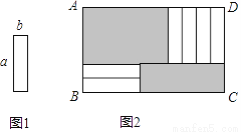
    A. a=2b B. a=3b C. a=4b D. a=b

    A 【解析】试题解析：如图， 左上角阴影部分的长为AE，宽为AF=3b，右下角阴影部分的长为PC，宽为a， ∵AD=BC，即AE+ED=AE+a，BC=BP+PC=4b+PC， ∴AE+a=4b+PC，即AE-PC=4b-a， ∴阴影部分面积之差S=AE•AF-PC•CG=3bAE-aPC=3b（PC+4b-a）-aPC=（3b-a）PC+12b2-3ab， 则3b-a=0，即...

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省中考数学一诊试卷 题型：单选题

    如图，在平面直角坐标系xOy中，△OAB的顶点A在x轴正半轴上，OC是△OAB的中线，点B、C在反比例函数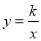（x＞0）的图象上，若△OAB的面积等于6，则k的值为（ ）

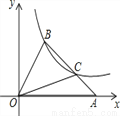
    A. 2 B. 4 C. 6 D. 8

    B 【解析】设A的坐标是（a，0），设B的坐标是（m，n）．则mn=k． ∵C是AB的中点， ∴C的坐标是（，）． ∵C在反比例函数上， ∴•=k，即（m+a）n=4k，mn+an=4k． ∵△OAB的面积是6， ∴an=6，即an=12， ∴k+12=4k， 解得k=4． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷（7） 题型：解答题

    如图，在?ABCD中，点E，F分别在边AD，BC上，点M，N在对角线AC上，且AE=CF，AM=CN，求证：四边形EMFN是平行四边形．

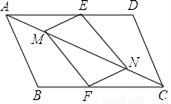
    证明见解析 【解析】试题分析：先由边角边证明△AEM≌△CFN ，得出EM=FN，EM∥FN即可解决问题． 试题解析：在平行四边形ABCD中，AD∥BC， ∴∠DAC=∠BCA， ∵AE=CF，AM=CN， ∴△AEM≌△CFN， ∴EM=FN，∠AME=∠CNF， ∴∠EMN=∠FNE， ∴EM∥FN， ∴四边形EMFN是平行四边形． ...

    查看答案和解析>>

    同步练习册答案