
在平面直角坐标系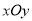 中,抛物线
中,抛物线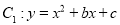 经过点
经过点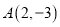 ,且与
,且与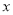 轴的一个交点为
轴的一个交点为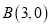 .
.
(1)求抛物线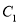 的表达式;
的表达式;
(2)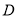 是抛物线
是抛物线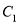 与
与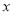 轴的另一个交点,点
轴的另一个交点,点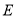 的坐标为
的坐标为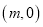 ,其中
,其中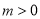 ,△
,△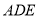 的面积为
的面积为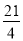 .
.
①求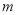 的值;
的值;
②将抛物线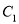 向上平移
向上平移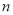 个单位,得到抛物线
个单位,得到抛物线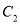 .若当
.若当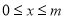 时,抛物线
时,抛物线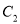 与
与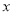 轴只有一个公共点,结合函数的图象,求
轴只有一个公共点,结合函数的图象,求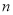 的取值范围.
的取值范围.
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷(7) 题型:解答题
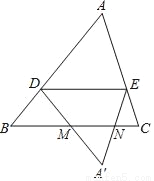
如图,在△ABC中,点D在边AB上(不与A,B重合),DE∥BC交AC于点E,将△ADE沿直线DE翻折,得到△A′DE,直线DA′,EA′分别交直线BC于点M,N.
(1)求证:DB=DM.
(2)若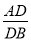 =2,DE=6,求线段MN的长.
=2,DE=6,求线段MN的长.
(3)若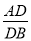 =n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
=n(n≠1),DE=a,则线段MN的长为 (用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源:山东省2018届九年级12月月考数学试卷 题型:单选题
如图,为测楼房BC的高,在距离楼房30米的A处测得楼顶的仰角为α,则楼高BC为( )

A.30tanα米
B.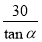 米
米
C.30sinα米
D.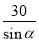 米
米
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:填空题
一元二次方程x2﹣4x=0的解是_____.
x1=0,x2=4. 【解析】x2﹣4x=0, x(x-4)=0, x1=0,x2=4. 故答案为x1=0,x2=4.查看答案和解析>>
科目:初中数学 来源:湖北省武汉市汉阳区2018届九年级(上)期中数学试卷(解析版) 题型:单选题
下列方程中,没有实数根的方程式( )
A. x2=9 B. 4x2=3(4x﹣1) C. x(x+1)=1 D. 2y2+6y+7=0
D 【解析】选项A. x2=9 ,解得x=. 选项B. 4x2=3(4x﹣1), 4x2-12x+3=0, .有解. 选项 C. x(x+1)=1 ,x2+x-1=0, .有解. 选项D. 2y2+6y+7=0, 无解. 所以选D.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:解答题
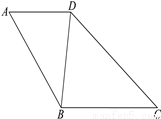
如图,在四边形ABCD中,AD∥BC,∠A=∠BDC.
(1)求证:△ABD∽△DCB;
(2)若AB=12,AD=8,CD=15,求DB的长.
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2016届九年级下学期二模数学试卷 题型:填空题
已知Rt△ABC,∠C=90°,AB=13,AC=12,以AC所在直线为轴将此三角形旋转一周所得圆锥的侧面积是________.(结果保留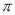 )
)
查看答案和解析>>
科目:初中数学 来源:2017年海南省海口市中考数学模拟试卷 题型:解答题
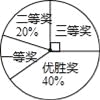
国务院办公厅在2015年3月16日发布了《中国足球发展改革总体方案》,这是中国足球史上的重大改革,为进一步普及足球知识,传播足球文化,我市某区在中小学举行了“足球在身边”知识竞赛,各类获奖学生人数的比例情况如图所示,其中获得三等奖的学生共50名,请结合图中信息,解答下列问题:
(1)获得一等奖的学生人数;
(2)在本次知识竞赛活动中,A,B,C,D四所学校表现突出,现决定从这四所学校中随机选取两所学校举行一场足球友谊赛,请用画树状图或列表的方法求恰好选到A,B两所学校的概率.
查看答案和解析>>
科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:单选题
在①﹣a5•(﹣a)2;②(﹣a6)÷(﹣a3);③(﹣a2)3•(a3)2;④[﹣(﹣a)2]5中计算结果为﹣a10的有( )
A. ①② B. ③④ C. ②④ D. ④
D 【解析】①原式=?,②原式=, ③原式= ,④原式=, 故选D查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com