
已知多边形每个内角都等于144°,则这个多边形是_________边形.
十(或10) 【解析】设这个多边形的边数为,由题意可得: , 解得: ,即这个多边形是十边形. 故答案为:十(或10). 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源:江苏省南通市崇川区2016-2017学年七年级上学期期末考试数学试卷 题型:单选题
下列判断中正确的是( )
A. 3a2bc与bca2不是同类项 B. 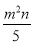 不是整式
不是整式
C. 单项式-x3y2的系数是-1 D. 3x2-y+5xy2是二次三项式
C 【解析】解:A.3a2bc与bca2是同类项,故错误; B. 是整式,故错误; C.单项式﹣x3y2的系数是﹣1,正确; D.3x2﹣y+5xy2是3次3项式,故错误. 故选C.查看答案和解析>>
科目:初中数学 来源:黑龙江省安达市校2017-2018学年七年级上册期末教学质量检测数学试卷 题型:填空题
如图,A,B,C,D,E,P,Q,R,S,T是构成五角星的五条线段的交点,则图中共有线段__条.
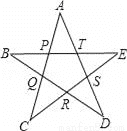
查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
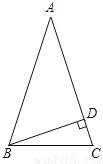
查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
计算:(-1)2017 +(π-3.14)0-(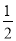 )3
)3
查看答案和解析>>
科目:初中数学 来源:云南省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下列语句正确的是( )
A. 三角形的三条高都在三角形内部 B. 三角形不一定具有稳定性
C. 三角形的三条中线交于一点 D. 三角形的角平分线可能在三角形的内部或外部
C 【解析】A选项,因为直角三角形和钝角三角形的高不全在三角形内部,所以A的说法错误; B选项,因为“三角形具有稳定性”,所以B中说法错误; C选项,因为“三角形三条中线是交于三角形内部一点的”,所以C中说法正确; D选项,因为“三角形的三条角平分线全在三角形内部”,所以D中说法错误; 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:解答题
某商品现在售价为每件60元,每星期可卖出300件,市场调查反映:调整价格,每件涨价1元,每星期要少卖出10件;每件降价1元,每星期可多卖出20件.已知商品的进价为每件40元.
(1)设每件降价x元,每星期的销售利润为y元;
① 请写出y与x之间的函数关系式;
② 确定x的值,使利润最大,并求出最大利润;
(2)若涨价x元,则x= 元时,利润y的最大值为 元(直接写出答案,不必写过程).
(1)①②x=2或3时y最大为6120;(2)5, 6250 【解析】试题分析:(1)①设每件降价x元,每星期的销售利润为y元,根据等量关系“总利润=每件的利润×每星期的销售量”,写出函数关系式即可;②把函数的解析式化为顶点式,然后根据x取整数,即可求得最大利润;(2)表示出商品的周销售量,根据等量关系“总利润=每件的利润×每星期的销售量”,写出函数关系式,再根据二次函数的性质求出最大利润即...查看答案和解析>>
科目:初中数学 来源:2017-2018学年度武汉市九年级元月联合测试数学试卷 题型:单选题
在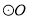 中,弦
中,弦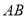 的长为6,圆心
的长为6,圆心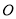 到
到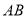 的距离为4,
的距离为4, 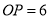 ,则点
,则点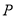 与
与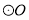 的位置关系是( )
的位置关系是( )
A. 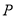 在
在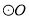 上 B.
上 B. 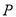 在
在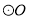 外 C.
外 C. 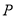 在
在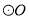 内 D.
内 D. 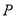 与
与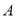 或
或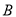 重合
重合
查看答案和解析>>
科目:初中数学 来源:上海市青浦区2018届九年级上学期期末调研测试数学试卷 题型:填空题
已知点D、E分别在△ABC的边BA、CA的延长线上,且DE∥BC,如果BC=3DE,AC=6,那么AE=_____.
2 【解析】∵DE//BC,∴△ADE∽△ABC, ∴AE:AC=DE:BC, ∵BC=3DE, ∴AE:AC=1:3, ∵AC=6, ∴AE=2, 故答案为:2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com