
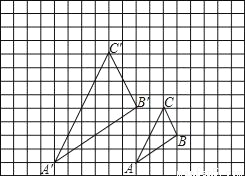
��ͼ��ͼ��С�����DZ߳�Ϊ1�������Σ���ABC���A��B��C���ǹ��ڵ�GΪλ�����ĵ�λ��ͼ�Σ����ǵĶ��㶼��С�����ζ����ϣ�
��1������λ�����ĵ�G��
��2������A��B��ƽ��ֱ������ϵ�е�����ֱ�Ϊ����6��0������-3��2������P��m��n�����߶�AC������һ�㣬���P�ڡ�A��B��C���ϵĶ�Ӧ��P�������Ϊ������
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ���һѧ����ĩ��ϰ����֮����ϰģ������꼶�˽̰���ѧ�Ծ���B���� ���ͣ������
��ͼ�����ɱ߳�Ϊ1����λ���ȵ�С�����ε������ڸ������һ��C��ʹ��ABC�ǵ��������Σ������ĵ�C��__����
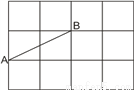
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�����СϪ����ѧ2017�������꼶��ѧ����ѧ�¼���� ���ͣ������
��֪ƽ���� ��
�� ��
��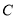 ��
��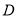 �ĸ��㣬������Ҫ��ͼ�Σ�
�ĸ��㣬������Ҫ��ͼ�Σ�
��1������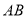 ��
��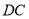 ��
��
��2����ֱ��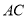 ��
��
��3��������DB��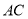 ��
��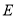 ��
��
��4���ӳ�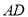 ��
��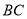 �ཻ��
�ཻ��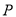 ��
��
��5���ֱ�ȡ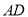 ��
��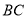 ���е�
���е�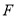 ��
�� ������
������ .
.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�����СϪ����ѧ2017�������꼶��ѧ����ѧ�¼���� ���ͣ���ѡ��
����������濴�����濴��ͼ, ��ȷ���� �� ��
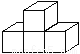

A. ��A�� B. ��B�� C. ��C�� D. ��D��
D �������������濴���õ���������3�������εĸ�������Ϊ1��2��1�� �����濴�õ�1�д��ϵ���2�������Ρ� ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶12���¿���ѧ�Ծ� ���ͣ������
��֪��O��ֱ��Ϊ10����A����B����C�ڡ�O�ϣ���CAB��ƽ���߽���O�ڵ�D��
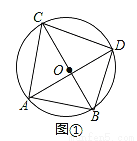
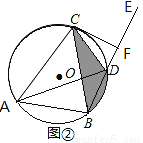
��1����ͼ�٣���BCΪ��O��ֱ����AB=6����AC��BD�ij���
��2����ͼ�ڣ�����CAB=60�㣬CF��BD������֤��CF�ǡ�O�����ߣ���������CD��CB�Լ���DBΧ��ͼ�ε������
��AC=8,BD=5���Ƣ�֤������������. �������������������1��Ҫ��AC�ij�����AC����Rt��ABC�У����ù��ɶ�������ã�Ҫ��BD�ij�����֤����BCDΪ����ֱ�������Σ��ٽ�Ϲ��ɶ������������2��������OC��֤����OCF=90�㼴�ɣ���ͨ��֤����CGD�ա�OGB�����Եõ�S��CGD=S��OGB���ɴ˽���Ӱ�������ת��Ϊ����DOB��������������������ʽ�������. ��������� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶12���¿���ѧ�Ծ� ���ͣ������
��ͼ������ABCD�У�AB=4��AD=3����Q�ڶԽ���AC�ϣ���AQ=AD������DQ���ӳ������BC���ڵ�P�����߶�AP=_________��
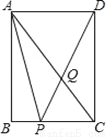
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶12���¿���ѧ�Ծ� ���ͣ������
������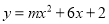 ��ͼ����x��ֻ��һ�������㣬��m=________.
��ͼ����x��ֻ��һ�������㣬��m=________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ2017-2018ѧ����꼶����ĩģ����ѧ�Ծ� ���ͣ������
����x�ķ���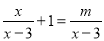 ����������m��ֵΪ________��
����������m��ֵΪ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ���Ƹ��й�����2017-2018ѧ�����꼶���ϣ�������ѧ�Ծ� ���ͣ������
�۲���������������������ɵı����ε�ʽ��
��1�㡡1+2=3
��2�㡡4+5+6=7+8
��3�㡡9+10+11+12=13+14+15
��4�㡡16+17+18+19+20=21+22+23+24
��
��1����գ���6��Ⱥ����ĵ�һ�������� ������n��Ⱥ��Ҳ���ұ����һ�������� �����ú�n��ʽ�ӱ�ʾ��n������������
��2�����99��Ⱥ��Ҳ��ұ�����������ֵĺͣ�
��3����������2017���ڵڼ��㣿��˵��������ι���ģ�
��1��43��n2+n+1����2����99���Ҳ�����������ֵĺ�Ϊ29994����3��2017���ڵ�44�� �������������������1��������֪����6��Ⱥ����ĵ�һ������62=36����n��Ⱥ����ĵ�һ������n2���ֱ����������1���ɵã����ݵ�n��ĵ�һ������n2����442��2016��452�ɵô𰸣� ��2�������Ϲ���֪��99���Ҳ������������Ϊ1002��1��1002��2��1002��3����ӿ�...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com