
计算:
(1)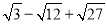 ; (2)(
; (2)(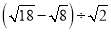 .
.
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
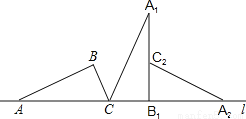
如图,把直角△ABC的斜边AC放在定直线l上,按顺时针的方向在直线l上转动两次,使它转到△A2B2C2的位置,设AB=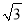 ,BC=1,则顶点A运动到点A2的位置时,点A所经过的路线为( )
,BC=1,则顶点A运动到点A2的位置时,点A所经过的路线为( )
A. (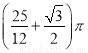 B.
B. 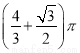 C. 2π D.
C. 2π D. 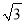 π
π
查看答案和解析>>
科目:初中数学 来源:2017年广东省东莞市堂星晨学校考数学模拟试卷 题型:解答题
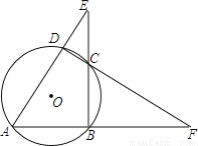
如图,⊙O的内接四边形ABCD两组对边的延长线分别交于点E、F.
(1)当∠E=∠F时,则∠ADC=_____°;
(2)当∠A=55°,∠E=30°时,求∠F的度数;
(3)若∠E=α,∠F=β,且α≠β.请你用含有α、β的代数式表示∠A的大小.
查看答案和解析>>
科目:初中数学 来源:2017年广东省东莞市堂星晨学校考数学模拟试卷 题型:单选题
今年,我市全面启动“精准扶贫”工作,某校为了了解九年级贫困生人数,对该校九年级6个班进行摸排,得到各班贫困生人数分别为:12,12,14,10,18,16,这组数据的众数和中位数分别是( ).
A. 12和10 B. 12和13 C. 12和12 D. 12和14
B 【解析】试题分析:∵12出现的次数最多,∴众数为12. 将这组数据按照从小到大的顺序排列:10、12、12、14、16、18. 中位数=(12+14)÷2=13. 故选B.查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:解答题
如图1,在正方形ABCD中,点E,F分别在AB,BC上,且AE=BF.
(1)试探索线段AF,DE的数量关系,写出你的结论并说明理由;
(2)连接EF,DF,分别取AE,EF,FD,DA的中点H,I,J,K,则四边形HIJK是什么特殊四边形?请在图2中补全图形,并说明理由.
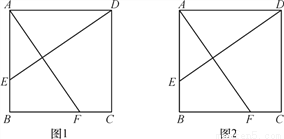
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:填空题
已知(x-y+3)2+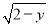 =0,则x+y=________.
=0,则x+y=________.
查看答案和解析>>
科目:初中数学 来源:2018年春人教版八年级数学下册(广西)期中测试 题型:单选题
估计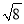 ×
×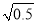 +
+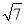 的运算结果在( )
的运算结果在( )
A. 3到4之间 B. 4到5之间 C. 5到6之间 D. 6到7之间
B 【解析】×+=, ∵4<7<9, ∴2<<3, ∴4<2+<5. 故选B.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 小题好拿分 题型:单选题
下列标志中,既是轴对称图形又是中心对称图形的为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:甘肃省定西市安定区2017-2018学年九年级上学期期末考试数学试卷 题型:填空题
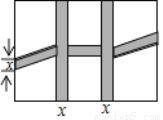
如图,某单位准备将院内一块长30m,宽20m的长方形花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图,要使种植花草的面积为532m2,设小道进出口的宽度为x m,根据条件,可列出方程:____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com