练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知x=2是一元二次方程x2+mx+2=0的一个解，则m的值是（ ）

    A. ﹣3 B. 3 C. 0 D. 0或3

    A 【解析】试题分析：∵x=2是一元二次方程x2+mx+2=0的一个解， ∴4+2m+2=0， ∴m=﹣3． 故选A．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年山东省中考数学二模试卷 题型：解答题

    某中学为促进课堂教学，提高教学质量，对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查．根据收回的问卷，学校绘制了如下图表，请你根据图表中提供的信息，解答下列问题．

    编号

    教学方式

    最喜欢的频数

    频率

    1

    教师讲，学生听

    20

    0.10

    2

    教师提出问题，学生探索思考

    3

    学生自行阅读教材，独立思考

    30

    4

    分组讨论，解决问题

    0.25

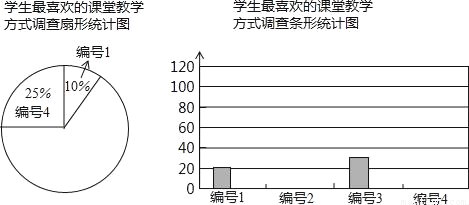
    （1）收回的问卷份数为　 　，把条形统计图补充完整；

    （2）扇形统计图中编号1与编号4的圆心角分别是多少度？

    （3）你最喜欢以上哪一种教学方式，请提出你的建议，并简要说明理由．

    （1）200，补图见解析;（2）编号1的圆心角是36°，编号4的圆心角是90°；（3）答案见解析. 【解析】试题分析：（1）根据编号1的数量及其百分比可得总人数，总人数乘以编号4的百分比求得其人数，总人数减去其他编号的数量求得编号2的人数，即可补全条形图； （2）用360°乘以其所占百分比即可得； （3）根据条形图各编号的具体人数，提出合理的建议均可． 试题解析：（1）收回...

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省苏州市中考数学三模试卷 题型：单选题

    已知两圆的直径分别为7和1，当它们相切时，圆心距为（　　）

    A. 8 B. 6 C. 8或6 D. 4或3

    D 【解析】试题解析：∵直径分别为7和1， ∴两圆半径分别为3.5和0.5， ∴当两圆外切时，圆心距为3.5+10.5=4； 当两圆内切时，圆心距为3.5?0.5=3. 故选D.

    查看答案和解析>>

    科目：初中数学 来源：福建省建瓯市2018届九年级数学上册期末测试卷 题型：填空题

    有四张正面分别标有数字－3，0，1，5的不透明卡片，它们除数字外其余全部相同．现将它们背面朝上，洗匀后从中任取一张，将该卡片上的数字记为a，则使关于x的分式方程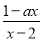＋2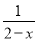＝有正整数解的概率为_____．

    【解析】试题解析：解分式方程得：x=， ∵x为正整数， ∴=1或=2（是增根，舍去）， 解得：a=0， 把a的值代入原方程解方程得到的方程的根为1， ∴能使该分式方程有正整数解的有1个， ∴使关于x的分式方程有正整数解的概率为.

    查看答案和解析>>

    科目：初中数学 来源：福建省建瓯市2018届九年级数学上册期末测试卷 题型：单选题

    如图，在4×4的正方形网格中，每个小正方形的边长为1，若将△AOC绕点O顺时针旋转90°得到△BOD，则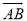的长为（ ）

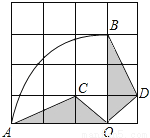
    A. π B. 6π C. 3π D. 1．5π

    D 【解析】试题分析： 的长==1.5π． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：解答题

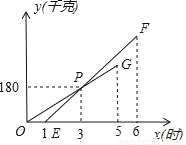
    某家装公司聘请两队搬运工来搬运货物，他们都只能连续搬运5小时，甲队于某日0时开始搬运，过了1小时，乙队也开始搬运，如图，线段OG表示甲队搬运量y（千克）与时间x（时）的函数图象，线段EF表示乙队搬运量y（千克）与时间x（时）的函数图象．

    （1）求乙队搬运量y与时间x之间的函数关系式．

    （2）如果甲、乙两队各连续搬运5小时，那么乙队比甲队多搬运多少千克？

    （1）y=90x﹣90；（2）乙队比甲队搬运150千克. 【解析】试题分析： （1）设乙队搬运量与搬运时间间的函数关系式为： ，由其图象经过点E（1，0）和点P（3，180）可列出方程组，解方程组求得的值即可得到所求解析式； （2）先根据图中信息求出甲队搬运量与搬运时间间的函数关系式，并计算出当=5时的函数值；再由（1）中所得函数解析式求出当时的函数值；用后者减去前者可得答案； ...

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷 题型：填空题

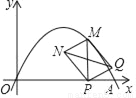
    如图，在平面直角坐标系中，抛物线y=﹣x2+4x与x轴交于点A，点M是x轴上方抛物线上一点，过点M作MP⊥x轴于点P，以MP为对角线作矩形MNPQ，连结NQ，则对角线NQ的最大值为_____．

    4 【解析】∵四边形MNPQ是矩形， ∴NQ=MP， ∴当MP最大时，NQ就最大. ∵点M是抛物线在轴上方部分图象上的一点，且MP⊥轴于点P， ∴当点M是抛物线的顶点时，MP的值最大. ∵， ∴抛物线的顶点坐标为（2，4）， ∴当点M的坐标为（2，4）时，MP最大=4， ∴对角线NQ的最大值为4.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年度第一学期海南省海口市七年级数学科期末检测模拟 题型：解答题

    某电动车厂一周计划生产2100辆电动车，平均每天计划生产300辆，由于各种原因，实际每天的生产量与计划量相比有出入．下表是某周的生产情况(超产为正，减产为负).

    星期

    一

    二

    三

    四

    五

    六

    日

    增减情况

    ＋5

    －2

    －4

    ＋13

    －10

    ＋16

    －9

    （1）根据记录可知本周前三天共生产电动车多少辆？

    （2）本周产量最多的一天比产量最少的一天多生产电动车多少辆？

    （3）该厂实行每周计件工资制，每生产一辆电动车可得a元，若超额完成，则超额部分每辆再奖b元(b＜a)，少生产一辆扣b元，求该厂工人这一周的工资总额.

    （注：第（1）、（2）小题列出算式，并计算）

    （1）899辆； （2）26辆；（3）(2109a+9b)元 【解析】（1）表示出三天的每一天生产的数量相加即可； （2）比较7个数据的大小，用最大的数据减去最小的数据即可； （3）算出一周的生产的总数量，与一周的计划产量相比写出代数式即可． 【解析】 （1）300×3+[(+5)+(-2)+(-4)]=899（辆）； （2）(+16)-(-10)=26（辆）； ...

    查看答案和解析>>

    科目：初中数学 来源：江苏省苏州市2017年中考数学二模试卷 题型：单选题

    某商店在节日期间开展优惠促销活动：购买原价超过200元的商品，超过200元的部分可以享受打折优惠．若购买商品的实际付款金额y（单位：元）与商品原价x（单位：元）的函数关系的图象如图所示，则超过200元的部分可以享受的优惠是（   ）

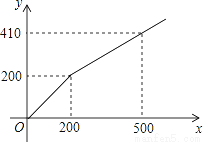
    A. 打八折 B. 打七折 C. 打六折 D. 打五折

    B 【解析】设， 把和代入， 得， ． ， ∴超过元部分打折． 故选：B.

    查看答案和解析>>

    同步练习册答案