
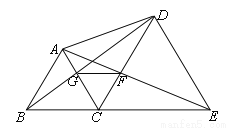
如图,已知B、C、E三点在同一条直线上,△ABC与△DCE都是等边三角形.其中线段BD交AC于点G,线段AE交CD于点F.
求证:(1)△ACE≌△BCD;(2)△GFC是等边三角形.
科目:初中数学 来源:浙江省杭州市2017-2018学年七年级上学期期中数学试卷 题型:解答题
把六张形状大小完全相同的小长方形卡片(其中较短的一边长为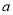 厘米,如图
厘米,如图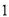 )不重叠地放在一个底面为长方形(长为
)不重叠地放在一个底面为长方形(长为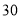 厘米,宽为
厘米,宽为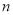 厘米)的盒子底部(如图
厘米)的盒子底部(如图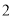 ),盒子底面未被卡片覆盖的部分分别用
),盒子底面未被卡片覆盖的部分分别用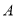 ,
, 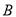 表示,请观察图形,回答问题:
表示,请观察图形,回答问题:
(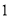 )求矩形
)求矩形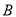 的长和宽(用含
的长和宽(用含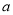 或
或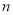 的代数式表示).
的代数式表示).
(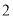 )当图中两块长方形阴影部分
)当图中两块长方形阴影部分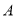 ,
, 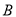 的周长和(用含
的周长和(用含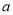 或
或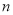 的代数式表示).
的代数式表示).
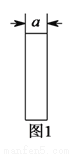
查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2017-2018学年八年级上学期期中数学试卷 题型:单选题
把点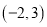 向上平移
向上平移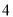 个单位长度,再向左平移
个单位长度,再向左平移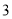 个单位长度,得到的点的坐标为( ).
个单位长度,得到的点的坐标为( ).
A. 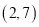 B.
B. 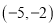 C.
C. 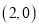 D.
D. 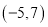
查看答案和解析>>
科目:初中数学 来源:福建省泉州台商投资区2017-2018学年七年级上学期期末教学质量检测数学试卷 题型:单选题
在桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,设组成这个几何体的小正方体的最少个数为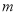 ,最多个数为
,最多个数为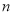 ,下列正确的是( )
,下列正确的是( )
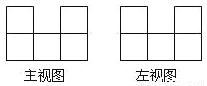
A. 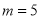 ,
, 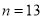 B.
B. 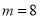 ,
, 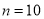
C. 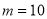 ,
, 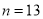 D.
D. 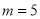 ,
, 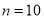
查看答案和解析>>
科目:初中数学 来源:福建省泉州台商投资区2017-2018学年七年级上学期期末教学质量检测数学试卷 题型:单选题
泉州台商投资区2017年生产总值预计可达到27600000000元人民币,这个数用科学记数法表示为( )
A. 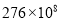 B.
B. 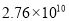 C.
C. 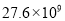 D.
D. 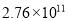
查看答案和解析>>
科目:初中数学 来源:山东省滨州市惠民县2017-2018学年八年级上学期期末数学试卷 题型:填空题
当x的值为_______________,分式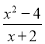 的值为0.
的值为0.
查看答案和解析>>
科目:初中数学 来源:山东省滨州市惠民县2017-2018学年八年级上学期期末数学试卷 题型:单选题
如果把分式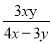 中的x和y的值都扩大为原来的3倍,那么分式的值
中的x和y的值都扩大为原来的3倍,那么分式的值
A. 扩大为原来的3倍 B. 扩大6倍
C. 缩小为原来的12倍 D. 不变
A 【解析】试题解析:分别用3x和3y去代换原分式中的x和y, 得, 可见新分式是原分式的3倍. 故选A.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市鄞州区九校2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
如图,直线y=-2x+2与x轴交于A点,与y轴交于B点.过点B作直线BP与x轴交于P点,若△ABP的面积是3,则P点的坐标是______
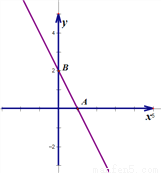
查看答案和解析>>
科目:初中数学 来源:福建省南平市2017-2018学年第一学期八年级期末质量检测数学试卷 题型:解答题
阅读材料:数学课上,吴老师在求代数式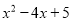 的最小值
的最小值
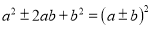 ,对式子作如下变
,对式子作如下变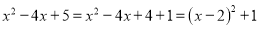 ,
,
因为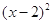 ≥0,所以
≥0,所以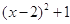 ≥1,当
≥1,当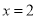 时,
时, 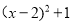 =1,
=1,
因此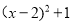 有最小值1,即
有最小值1,即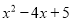 的最小值为1.
的最小值为1.
通过阅读,解下列问题:
(1)代数式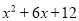 的最小值为 ;
的最小值为 ;
(2)求代数式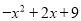 的最大或最小值;
的最大或最小值;
(3)试比较代数式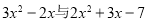 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com