
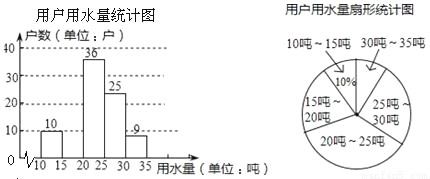
某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:单选题
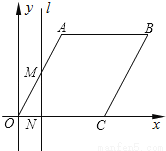
如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( )
A.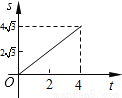 B.
B.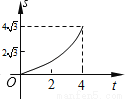
C.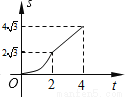 D.
D.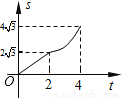
查看答案和解析>>
科目:初中数学 来源:2017年内蒙古乌兰察布市中考数学一模试卷 题型:解答题
我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;并求出自变量x的取值范围;
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
(1)y=﹣5x+2200(300≤x≤350);(2)售价定为320元/台时,商场每月销售这种空气净化器所获得的利润w最大,最大利润是72000元 【解析】试题分析:(1)、销售量=200+50×(降价的数量÷10)得出答案;(2)、根据供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台,得出不等式组,从而得出x的取值范围;(3)、根据总利润=单件利润×数...查看答案和解析>>
科目:初中数学 来源:2017年内蒙古乌兰察布市中考数学一模试卷 题型:单选题
一个袋子中装有3个红球和2个黄球,这些球的形状、大小.质地完全相同,在看不到球的条件下,随机从袋子里同时摸出2个球,其中2个球的颜色相同的概率是( )
A. 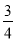 B.
B. 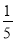 C.
C. 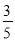 D.
D. 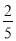
查看答案和解析>>
科目:初中数学 来源:2017年江苏省徐州市中考数学模拟试卷(2) 题型:解答题
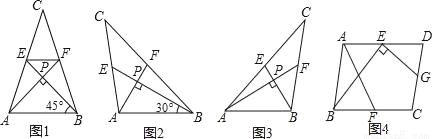
我们把两条中线互相垂直的三角形称为“中垂三角形”,例如图1,图2,图3中,AF,BE是△ABC的中线,AF⊥BE,垂足为P,像△ABC这样的三角形均为“中垂三角形”,设BC=a,AC﹣b,AB=c.
【特例探索】
(1)如图1,当∠ABE=45°,c=2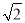 时,a= ,b= ;如图2,当∠ABE=30°,c=4时,a= ,b= ;
时,a= ,b= ;如图2,当∠ABE=30°,c=4时,a= ,b= ;
【归纳证明】
(2)请你观察(1)中的计算结果,猜想a2,b2,c2三者之间的关系,用等式表示出来,请利用图3证明你发现的关系式;
【拓展应用】
(3)如图4,在?ABCD中,点E,F,G分别是AD,BC,CD的中点,BE⊥EG,AD=2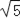 ,AB=3.求AF的长.
,AB=3.求AF的长.
查看答案和解析>>
科目:初中数学 来源:2017年江苏省徐州市中考数学模拟试卷(2) 题型:填空题
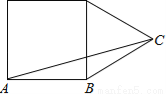
边长为1的一个正方形和一个等边三角形如图摆放,则△ABC的面积为 .
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年七年级数学上期末复习检测数学试卷 题型:填空题
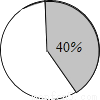
如图是地球表面的一部分,扇形A表示地球某几种水域占总面积的40%,则此扇形的圆心角为________.
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(十) 题型:单选题
如图是2014年巴西世界杯吉祥物,某校在五个班级中对认识它的人数进行了调查,结果为(单位:人):30,31,27,26,31.这组数据的中位数是( )

A. 27 B. 29 C. 30 D. 31
C 【解析】中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数)。由此将这组数据重新排序为26,27,30,31,31,∴中位数是按从小到大排列后第3个数为:30。故选C。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com