
如图,在平面直角坐标系中,四边形OABC是菱形,点C的坐标为(4,0),∠AOC=60°,垂直于x轴的直线l从y轴出发,沿x轴正方向以每秒1个单位长度的速度向右平移,设直线l与菱形OABC的两边分别交于点M,N(点M在点N的上方),若△OMN的面积为S,直线l的运动时间为t 秒(0≤t≤4),则能大致反映S与t的函数关系的图象是( )
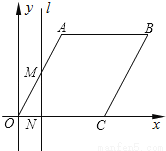
A.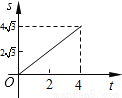 B.
B.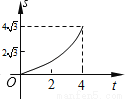
C.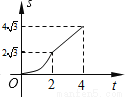 D.
D.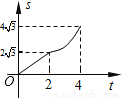
科目:初中数学 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:单选题
每年的4月23日是“世界读书日”.某中学为了了解八年级学生的读书情况,随机调查了50名学生的册数,统计数据如表所示:
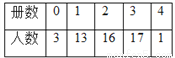
则这50名学生读数册数的众数、中位数是( )
A. 3,3 B. 3,2 C. 2,3 D. 2,2
B 【解析】∵这组样本数据中,3出现了17次,出现的次数最多, ∴这组数据的众数是3. ∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都是2,有=2, ∴这组数据的中位数为2; 故选B.查看答案和解析>>
科目:初中数学 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:填空题
已知二次函数y=ax2+bx+c(a≠0),其中a,b,c满足a+b+c=0和9a﹣3b+c=0,则该二次函数图象的对称轴是直线 .
x=﹣1. 【解析】 试题分析:解方程求出a,b的值,再根据对称轴公式即可求出该二次函数图象的对称轴. 【解析】 方程9a﹣3b+c=0减去方程a+b+c=0, 可得8a﹣4b=0, 根据对称轴公式整理得:对称轴为x==﹣1. 故该二次函数图象的对称轴是直线x=﹣1.查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:解答题
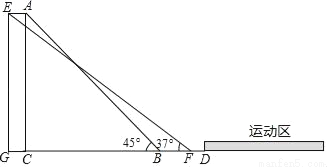
某学校为增加体育馆观众坐席数量,决定对体育馆进行施工改造.如图,为体育馆改造的截面示意图.已知原座位区最高点A到地面的铅直高度AC长度为15米,原坡面AB的倾斜角∠ABC为45°,原坡脚B与场馆中央的运动区边界的安全距离BD为5米.如果按照施工方提供的设计方案施工,新座位区最高点E到地面的铅直高度EG长度保持15米不变,使A、E两点间距离为2米,使改造后坡面EF的倾斜角∠EFG为37°.若学校要求新坡脚F需与场馆中央的运动区边界的安全距离FD至少保持2.5米(即FD≥2.5),请问施工方提供的设计方案是否满足安全要求呢?请说明理由.(参考数据:sin37°≈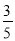 ,tan37°≈
,tan37°≈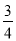 )
)
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:填空题
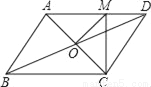
如图,□ABCD的周长为16cm,AC、BD交于点O,且AD>CD,过O作OM⊥AC,交AD于点M,则△CDM的周长为_____cm.
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷 题型:单选题
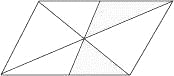
如图所示,在平行四边形纸片上作随机扎针实验,针头扎在阴影区域内的概率为( )
A. 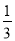 B.
B. 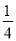 C.
C. 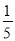 D.
D. 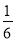
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型:解答题
已知抛物线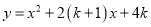 .
.
(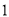 )求证:不论
)求证:不论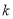 取何值,抛物线
取何值,抛物线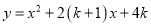 与
与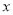 轴有交点.
轴有交点.
(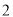 )若抛物线
)若抛物线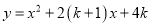 与
与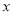 轴有两个交点,且这两个交点分别在直线
轴有两个交点,且这两个交点分别在直线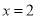 的两侧,求
的两侧,求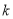 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型:单选题
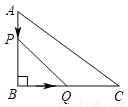
如图,在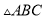 中,
中, 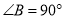 ,
, 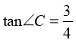 ,
, 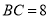 .动点
.动点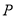 从点
从点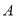 开始沿边
开始沿边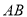 向点
向点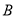 以
以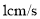 的速度移动,动点
的速度移动,动点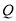 从点
从点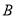 开始沿边
开始沿边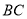 向点
向点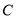 以
以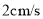 的速度移动.若
的速度移动.若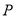 ,
, 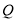 两点分别从
两点分别从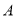 ,
, 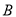 两点同时出发,在运动过程中,
两点同时出发,在运动过程中, 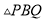 的最大面积是( ).
的最大面积是( ).
A. 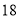 B.
B. 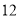 C.
C. 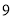 D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017年江苏省徐州市中考数学模拟试卷(2) 题型:解答题
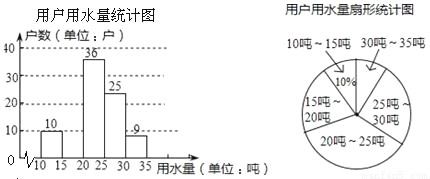
某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地做决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如图不完整的统计图(每组数据包括最大值但不包括最小值),请你根据统计图解决下列问题:
(1)此次抽样调查的样本容量是
(2)补全左侧统计图,并求扇形统计图中“25吨~30吨”部分的圆心角度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com