
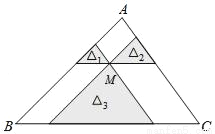
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是 .
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
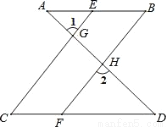
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.请说明理由
查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:填空题
分解因式:x2y﹣4y= .
【解析】试题分析:先提取公因式y,然后再利用平方差公式进行二次分解. 【解析】 x2y﹣4y, =y(x2﹣4), =y(x+2)(x﹣2). 故答案为:y(x+2)(x﹣2).查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学全册综合测试卷 题型:单选题
若分式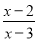 有意义,则
有意义,则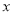 满足的条件是( )
满足的条件是( )
A. 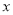 ≠0 B.
≠0 B. 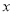 ≠2 C.
≠2 C. 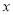 ≠3 D.
≠3 D. 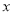 ≥3
≥3
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.2 实际问题与反比例函数(第2课时) 题型:解答题
某学校冬季储煤120吨,若每天用煤 x吨,经过 y天可以用完.
(1)请与出 y与 x之间的函数关系式;
(2)画出函数的图象;
(3)当每天的用煤量为1.2~1.5吨时,这些煤可用的天数在什么范围?
(1) y= ;(2)详见解析;(3) . 【解析】试题分析: (1)由“煤燃烧的天数=储煤量÷每天烧煤的吨数”即可得到y与 x之间的函数关系式; (2)由(1)中所得函数关系式,画出对应的函数图象即可; (3)将和代入(1)中所得函数关系式求得对应的的值即可得到可用天数的取值范围. 试题解析: (1)由“煤燃烧的天数=储煤量÷每天烧煤的吨数”可得y与 x之间的...查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:解答题
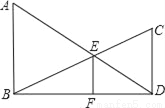
已知:如图,AB⊥BD,CD⊥BD,垂足分别为B、D,AD和BC相交于点E,EF⊥BD,垂足为F,我们可以证明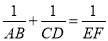 成立(不要求考生证明).
成立(不要求考生证明).
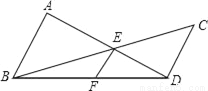
若将图中的垂线改为斜交,如图,AB∥CD,AD,BC相交于点E,过点E作EF∥AB交BD于点F,则:
(1)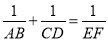 还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
还成立吗?如果成立,请给出证明;如果不成立,请说明理由;
(2)请找出S△ABD,S△BED和S△BDC间的关系式,并给出证明.
查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:填空题
小刚和小明在太阳光下行走,小刚身高1.75米,他的影长为2.0m,小刚比小明矮5cm,此刻小明的影长是________m.
【解析】本题考查相似三角形性质的应用 在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似. 如图, ∵小刚身高1.75米,小刚比小明矮5cm, ∴小明的身高为, ∵△ADE∽△ABC 设小明的影长是x,则查看答案和解析>>
科目:初中数学 来源:2018届九年级中考数学专题复习同步练习题:平行四边形 题型:解答题
已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.
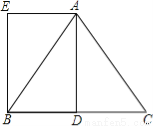
(1)求证:四边形ADBE是矩形;
(2)求矩形ADBE的面积.
(1)证明见解析;(2)12. 【解析】 试题分析:(1)利用三线合一定理可以证得∠ADB=90°,根据矩形的定义即可证得; (2)利用勾股定理求得BD的长,然后利用矩形的面积公式即可求解. 试题解析: (1)∵AB=AC,AD是BC的边上的中线, ∴AD⊥BC, ∴∠ADB=90°, ∵四边形ADBE是平行四边形. ∴平行四边形ADBE是矩形; ...查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:单选题
一组数据:0,1,2,3,3,5,5,10的中位数是( ).
A. 2.5 B. 3 C. 3.5 D. 5
B 【解析】试题分析:根据中位数的定义先把这组数据从小到大排列,再求出最中间两个数的平均数即可.将这组数据从小到大排列为:0,1,2,3,3,5,5,10,最中间两个数的平均数是:(3+3)÷2=3,则中位数是3; 故选:B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com