
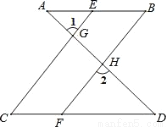
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.请说明理由
 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源:浙江杭州西湖区公益中学2017-2018学年八年级上学期期中数学 题型:单选题
如图,在 中,
中,  ,以
,以 的一边为边画等腰三角形,使得它的第三个顶点在
的一边为边画等腰三角形,使得它的第三个顶点在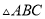 的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
的其他边上,则可以画出的不同的等腰三角形的个数最多为( )
A. 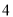 B.
B. 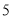 C.
C. 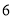 D.
D. 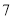
查看答案和解析>>
科目:初中数学 来源:人教版八年级下册数学全册综合测试卷 题型:填空题
如图,它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形,如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值为 .
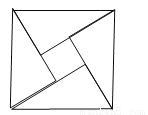
查看答案和解析>>
科目:初中数学 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
如图,已知AB∥CD,分别探讨下面四个图形中∠APC与∠PAB,∠PCD之间的关系,请你从所得到的关系中任选一个加以证明。
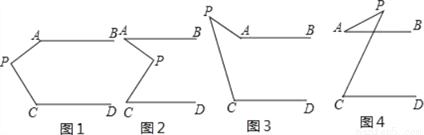
(1)在图1中,∠APC与∠PAB,∠PCD之间的关系是: .
(2)在图2中,∠APC与∠PAB,∠PCD之间的关系是: .
(3)在图3中,∠APC与∠PAB,∠PCD之间的关系是: .
(4)在图4中,∠APC与∠PAB,∠PCD之间的关系是: .
(5)在图 中,求证: .
答案见解析 【解析】试题分析:(1)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,即可求得答案; (2)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案; (3)由AB∥CD,根据两直线平行,同位角线相等,以及三角形外角的性质,即可求得答案; (4)由AB∥CD,根据...查看答案和解析>>
科目:初中数学 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
如图,已知AB∥CD,∠ABE和∠CDE的平分线相交于F,∠E = 140º,求∠BFD的度数.
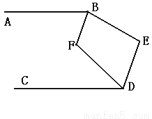
查看答案和解析>>
科目:初中数学 来源:人教版 2018年春 七年级数学下册 第五章 相交线与平行线 几何证明题 题型:解答题
如图,DB∥FG∥EC,∠ABD=60°,∠ACE=36°,AP平分∠BAC.求∠PAG的度数.
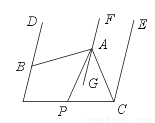
查看答案和解析>>
科目:初中数学 来源:人教版七年级下册 第1-3章 综合测试卷 题型:填空题
如图,将周长为16的三角形  沿
沿 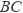 方向平移3个单位得到三角形
方向平移3个单位得到三角形 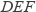 ,则四边形
,则四边形 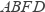 的周长等于 ________.
的周长等于 ________.

查看答案和解析>>
科目:初中数学 来源:人教版七年级下册 第1-3章 综合测试卷 题型:单选题
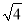 的值是( )
的值是( )
A. 4 B. 2 C. ±2 D. 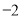
查看答案和解析>>
科目:初中数学 来源:广东省2017-2018学年度九年级(上)数学第一次月考试卷(11月份)(解析版) 题型:解答题
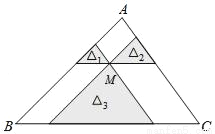
如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com