
已知线段AB=8厘米,在直线上作线段BC,使它等于3厘米,则线段AC=_____厘米.
5或11 【解析】根据题意,点C可能在线段AB上,也可能在AB的延长线上.可分类讨论为: 若点C在线段AB上,则AC=AB﹣BC=8﹣3=5(cm); 若点C在AB的延长线上,则AC=AB+BC=8+3=11(cm). 故答案为:5或11. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:辽宁省葫芦岛市建昌县2017-2018学年八年级上学期期末测评数学试卷 题型:填空题
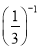
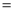 ______;
______; 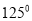
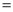 _______
_______
查看答案和解析>>
科目:初中数学 来源:2018年河南省驻马店市第一次中考模拟数学试卷 题型:解答题
(8分)已知AB为⊙O的直径,OC⊥AB,弦DC与OB交于点F,在直线AB上有一点E,连接ED,且有ED=EF.
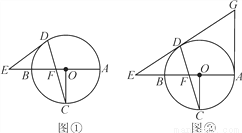
(1)如图①,求证:ED为⊙O的切线;
(2)如图②,直线ED与切线AG相交于G,且OF=2,⊙O的半径为6,求AG的长.
(1)见解析;(2)12 【解析】试题分析:(1)连接OD,由ED=EF可得出∠EDF=∠EFD,由对顶角相等可得出∠EDF=∠CFO;由OD=OC可得出∠ODF=∠OCF,结合OC⊥AB即可得知∠EDF+∠ODF=90°,即∠EDO=90°,由此证出ED为⊙O的切线; (2)连接OD,过点D作DM⊥BA于点M,结合(1)的结论根据勾股定理可求出ED、EO的长度,结合∠DOE的正弦、余...查看答案和解析>>
科目:初中数学 来源:2018年河南省驻马店市第一次中考模拟数学试卷 题型:单选题
如图,AB为⊙O的直径,点C在⊙O上,连接AC,OC,过点B作BD⊥OC,交⊙O于点D,已知∠ACO=35°,则∠COD的度数为( )
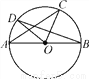
A. 70° B. 60° C. 45° D. 35°
A 【解析】【解析】 ∵OA=OC,∴∠OAC=∠ACO=35°,∴∠BOC=2∠A=70°.∵BD⊥OC,∴弧CD =弧BC,∴∠COD=∠BOC=70°.故选A.查看答案和解析>>
科目:初中数学 来源:山东省潍坊市高密市2017-2018学年七年级(上)期中数学试卷 题型:解答题
阅读下列第(1)题中的计算方法,再计算第(2)题中式子的值.
(1)﹣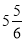 +(﹣9
+(﹣9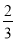 )+17
)+17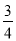 +(﹣3
+(﹣3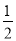 )
)
【解析】
原式=[(﹣5)+(﹣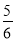 )]+[(﹣9)+(﹣
)]+[(﹣9)+(﹣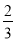 )]+[(+17)+(+
)]+[(+17)+(+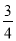 )]+[(﹣3)+(﹣
)]+[(﹣3)+(﹣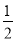 )]
)]
=[(﹣5)+(﹣9)+(+17)+(﹣3)]+[(﹣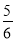 )+(﹣
)+(﹣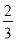 )+(+
)+(+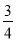 )+(﹣
)+(﹣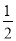 )]
)]
=0+(﹣1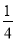 )
)
=﹣1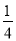
上面这种方法叫拆项法.仿照上述方法计算:
(2)(﹣2008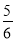 )+(﹣2007
)+(﹣2007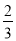 )+4017
)+4017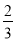 +(﹣1
+(﹣1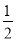 )
)
查看答案和解析>>
科目:初中数学 来源:山东省潍坊市高密市2017-2018学年七年级(上)期中数学试卷 题型:填空题
计算﹣2﹣5=_____.
-7 【解析】根据减法法则,﹣2﹣5就是﹣2与﹣5的和,即﹣2+(﹣5),再根据加法法则解题可得:﹣2﹣5=﹣2+(﹣5)=﹣7. 故答案为:-7.查看答案和解析>>
科目:初中数学 来源:山东省潍坊市高密市2017-2018学年七年级(上)期中数学试卷 题型:单选题
下列说法中,正确的有( )个
①两个有理数的和不小于每个加数
②两个有理数的差不大于被减数
③互为相反数的两个数,它们的平方相等
④多个有理数相乘,当负因数有奇数个时积为负.
A. 0 B. 1 C. 2 D. 3
B 【解析】利用有理数的乘法,加法,减法法则判断: ①两个有理数的和不一定小于每个加数,不正确; ②两个有理数的差不一定大于被减数,不正确; ③互为相反数的两个数,它们的平方相等,正确; ④多个有理数相乘(0除外),当负因数有奇数个时积为负,不正确. 故选:B.查看答案和解析>>
科目:初中数学 来源:浙江省余姚市2018届九年级上学期期中考试数学试卷 题型:填空题
飞机着陆后滑行的距离s(单位:米)关于滑行的时间t(单位:秒)的函数解析式是s=60t-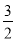 t2,则飞机着陆后滑行的最长时间为________秒;
t2,则飞机着陆后滑行的最长时间为________秒;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com