
计算下列各题:
(1)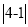 -3=_______; (2)
-3=_______; (2)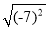 =_______; (3)50=______; (4)
=_______; (3)50=______; (4)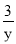 +
+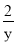 =__________.
=__________.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:江苏省无锡市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
某立体图形的三视图均相同,则该立体图形可能是( )
A. 圆锥 B. 球 C. 圆柱 D. 四棱锥
B 【解析】试题解析:球的三视图都是圆形,三视图均相同,故该立体图形可能是球. 故选B.查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
若关于x的分式方程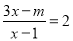 的解是正数,则m的取值范围为_______.
的解是正数,则m的取值范围为_______.
查看答案和解析>>
科目:初中数学 来源:2017-2018年福建厦门市八年级上册数学期末质量检测试卷 题型:解答题
已知一组数9,17,25,33,…,(8n+1)(从左往右数,第1个数是9,第2个数是17,第3个数是25,第4个数是33,依此类推,第n个数是8n+1).设这组数的前n个数的和是sn.
(1)第5个数是多少?并求1892—s5的值;
(2)若n满足方程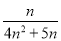 =
=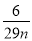 ,则
,则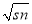 的值是整数吗?请说明理由.
的值是整数吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源:2017-2018年福建厦门市八年级上册数学期末质量检测试卷 题型:填空题
如图,在河流的同岸有A,B两个村庄,要在河岸l上确定相距a米的两点C,D(点D在点C的右边),使得AC+BD的和最小.若用作图的方式来确定点C,则确定点C的步骤是______________.

查看答案和解析>>
科目:初中数学 来源:2017-2018年福建厦门市八年级上册数学期末质量检测试卷 题型:单选题
如图,在长方形ABCD中,点E在边BC上,过点E作EF⊥AD,垂足为F,若EF=BE,则下列结论中正确的是( )
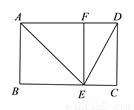
A. EF是∠AED的角平分线 B. DE是∠FDC的角平分线
C. AE是∠BAF的角平分线 D. EA是∠BED的角平分线
C 【解析】试题解析:∵四边形ABCD是长方形, ∴BE⊥AB ∵EF⊥AD,且EF=BE ∴AE是∠BAF的角平分线 故选C.查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型:解答题
某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为20℃的条件下生长最快的新品种.图示是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是反比例函数y=一的图象上一部分,请根据图中信息解答下列问题
(1)恒温系统在这天保持大棚内温度20℃的时间有多少小时?
(2)求k的值;
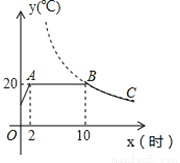
(3)当x=20时,大棚内的温度约为多少度?
【答案】(1)8小时;(2)200;(3)当x=20时,大棚内的温度约为10℃.
【解析】试题分析:(1)根据图象直接得出大棚温度20℃的时间为10﹣2=8(小时);
(2)利用待定系数法求反比例函数解析式即可;
(3)将x=20代入函数解析式求出y的值即可.
试题解析:(1)恒温系统在这天保持大棚温度20℃的时间为:10﹣2=8(小时);
(2)∵点B(10,20)在双曲线y=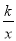 上,
上,
∴20=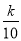 ,
,
∴解得:k=200;
(3)当x=20时,y=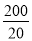 =10,
=10,
所以当x=20时,大棚内的温度约为10℃.
【点睛】本题考查了反比例函数的应用,正确地求得反比例函数的解析式是解题的关键.
【题型】解答题
【结束】
25
某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过x min时,A、B两组材料的温度分别为yA℃、yB℃,yA、yB与x的函数关系式分别为yA=kx+b,yB=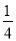 (x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
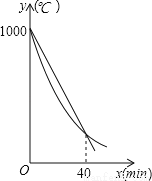
(1)分别求yA、yB关于x的函数关系式;
(2)当A组材料的温度降至120℃时,B组材料的温度是多少?
(3)在0<x<40的什么时刻,两组材料温差最大?
(1)yA=﹣20x+1000; (2)B组材料的温度是164℃; (3)当x=20时,两组材料温差最大为100℃. 【解析】试题分析:(1)首先求出yB函数关系式,进而得出交点坐标,即可得出yA函数关系式;(2)首先将y=120代入求出x的值,进而代入yB求出答案;(3)得出yA-yB的函数关系式,进而求出最值即可. 试题解析:(1)由题意可得出:yB=(x﹣60)2+m...查看答案和解析>>
科目:初中数学 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型:单选题
如图,在Rt△ABC中,∠ACB=90°,BC=2,AB=4,则下列结论正确的是( )
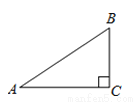
A. cosB=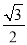 B. tanA=
B. tanA=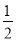 C. tanB=
C. tanB=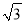 D. sinB=
D. sinB=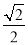
查看答案和解析>>
科目:初中数学 来源:2017-2018学年苏州市、吴江、相城七年级第一学期期末数学统考试卷 题型:填空题
已知点C是线段AB的中点,点D在直线AB上,BD=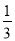 AB,若AD=16,则CD=_________.
AB,若AD=16,则CD=_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com