
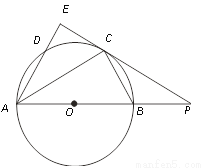
如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且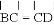 ,弦AD的延长线交切线PC于点E,连接BC.
,弦AD的延长线交切线PC于点E,连接BC.
(1)判断OB和BP的数量关系,并说明理由;
(2)若⊙O的半径为2,求AE的长.
 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源:2017年海南省中考数学模拟试卷(三) 题型:填空题
已知点P(a﹣1,a+2)在平面直角坐标系的第二象限内,则a的取值范围是( )
A. 1<a<2 B. ﹣1<a<2 C. ﹣2<a<﹣1 D. ﹣2<a<1
D 【解析】试题解析:∵点P(a?1,a+2)在平面直角坐标系的第二象限内, 解不等式①得,a<1, 解不等式②得,a>?2, ∴?2查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区杭州外国语学校2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:解答题
已知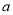 ,
, 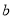 ,
, 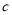 在数轴上的对应点如图所示:
在数轴上的对应点如图所示:
(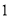 )根据数轴判断:
)根据数轴判断: 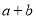 __________
__________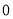 ,
, 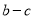 __________
__________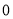 .(填
.(填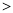 ,
, 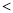 ,
, 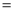 )
)
(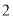 )化简:
)化简: 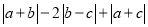 .
.

查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区杭州外国语学校2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:单选题
若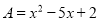 ,
, 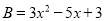 ,则
,则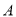 与
与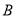 的大小关系是( ).
的大小关系是( ).
A. 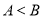 B.
B. 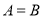 C.
C. 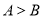 D. 无法确定
D. 无法确定
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学二模试卷 题型:解答题
已知抛物线y=ax2-2ax+c与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且OC=3OA.
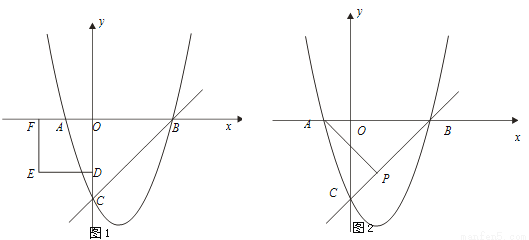
(1)求抛物线的函数表达式;
(2)直接写出直线BC的函数表达式;
(3)如图1,D为y轴的负半轴上的一点,且OD=2,以OD为边作正方形ODEF.将正方形ODEF以每秒1个单位的速度沿x轴的正方向移动,在运动过程中,设正方形ODEF与△OBC重叠部分的面积为s,运动的时间为t秒(0<t≤2).
求:①s与t之间的函数关系式;
②在运动过程中,s是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(4)如图2,点P(1,k)在直线BC上,点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的平行四边形?若存在,请直接写出M点坐标;若不存在,请说明理由.
(1)y=x2-2x-3 ; (2)直线BC的函数表达式为y=x-3; (3)① ②当t =2秒时,S有最大值,最大值为. (4)存在符合条件的点M,且坐标为M 1(-,),M2(,), M3(,),M4(,) 【解析】分析:(1)先由OC、OA的数量关系确定点C的坐标,然后利用待定系数法可求出抛物线的解析式; (2)由(1)的抛物线解析式可得点B的坐标,结合点C的坐...查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学二模试卷 题型:填空题
如图,边长为6的正方形ABCD内部有一点P,BP=4,∠PBC=60°,点Q为正方形边上一动点,且△PBQ是等腰三角形,则符合条件的Q点有__________个.

查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学二模试卷 题型:填空题
如图,直线a∥b,∠1=60° ,则∠2=__________°.
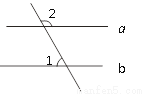
查看答案和解析>>
科目:初中数学 来源:上海市2016-2017学年度第一学期八年级期末考试试卷 题型:填空题
已知在等腰三角形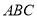 中,
中, 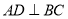 于点
于点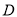 ,且
,且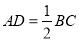 ,那么
,那么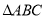 的底角等于__________________.
的底角等于__________________.
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2016-2017学年七年级下学期期末考试数学试卷 题型:单选题
如果 ,且
,且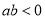 ,那么( )
,那么( )
A. 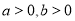 B.
B. 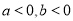
C. 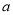 、
、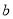 异号且正数的绝对值较小 D.
异号且正数的绝对值较小 D. 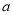 、
、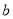 异号且负数的绝对值较小
异号且负数的绝对值较小
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com