
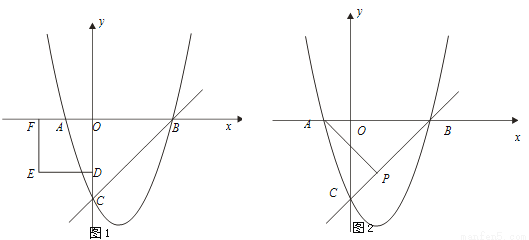
已知抛物线y=ax2-2ax+c与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且OC=3OA.
(1)求抛物线的函数表达式;
(2)直接写出直线BC的函数表达式;
(3)如图1,D为y轴的负半轴上的一点,且OD=2,以OD为边作正方形ODEF.将正方形ODEF以每秒1个单位的速度沿x轴的正方向移动,在运动过程中,设正方形ODEF与△OBC重叠部分的面积为s,运动的时间为t秒(0<t≤2).
求:①s与t之间的函数关系式;
②在运动过程中,s是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(4)如图2,点P(1,k)在直线BC上,点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的平行四边形?若存在,请直接写出M点坐标;若不存在,请说明理由.
(1)y=x2-2x-3 ; (2)直线BC的函数表达式为y=x-3; (3)① ②当t =2秒时,S有最大值,最大值为. (4)存在符合条件的点M,且坐标为M 1(-,),M2(,), M3(,),M4(,) 【解析】分析:(1)先由OC、OA的数量关系确定点C的坐标,然后利用待定系数法可求出抛物线的解析式; (2)由(1)的抛物线解析式可得点B的坐标,结合点C的坐... 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源:2017年海南省中考数学模拟试卷(三) 题型:单选题
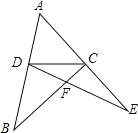
如图,在△ABC、△ADE中,C、D两点分别在AE、AB上,BC、DE交于点F,若BD=DC=CE,∠ADC+∠ACD=114°,则∠DFC为( )
A.114° B.123° C.132° D.147°
B. 【解析】 试题分析:∵BD=CD=CE,等腰三角形的性质得出∠B=∠DCB,∠E=∠CDE, ∵∠ADC+∠ACD=114°,∴∠BDC+∠ECD=360°﹣114°=246°, ∴∠B+∠DCB+∠E+∠CDE=360°﹣246°=114°, ∴∠DCB+∠CDE=57°, ∴∠DFC=180°﹣57°=123°, 故选B.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 七年级数学 小题好拿分 题型:单选题
下列各式中是一元一次方程的是( )
A. 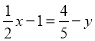 B. -5-3=-8 C. x+3 D.
B. -5-3=-8 C. x+3 D. 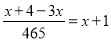
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区杭州外国语学校2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:填空题
据国家旅游局消息, 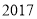 年国庆中秋假日旅游市场供给充足、需求旺盛、运行平稳、安全有序,全国未发生重大旅游安全事故,无重大旅游投诉,全国共接待国内游客约
年国庆中秋假日旅游市场供给充足、需求旺盛、运行平稳、安全有序,全国未发生重大旅游安全事故,无重大旅游投诉,全国共接待国内游客约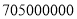 人数,请将数字
人数,请将数字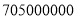 用科学计数法表示为__________.
用科学计数法表示为__________.
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区杭州外国语学校2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:单选题
估计实数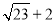 的值,它的所在范围是( ).
的值,它的所在范围是( ).
A. 在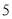 和
和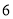 之间 B. 在
之间 B. 在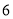 和
和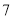 之间 C. 在
之间 C. 在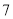 和
和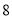 之间 D. 在
之间 D. 在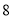 和
和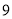 之间
之间
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学二模试卷 题型:解答题
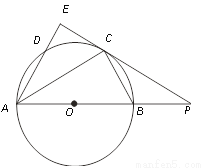
如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且 ,弦AD的延长线交切线PC于点E,连接BC.
,弦AD的延长线交切线PC于点E,连接BC.
(1)判断OB和BP的数量关系,并说明理由;
(2)若⊙O的半径为2,求AE的长.
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学二模试卷 题型:填空题
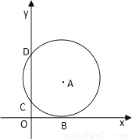
如图,在平面直角坐标系中,点A在第一象限,⊙A与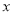 轴相切于B,与
轴相切于B,与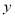 轴交于C(0,1)、D(0,4)两点,则点A的坐标是 .
轴交于C(0,1)、D(0,4)两点,则点A的坐标是 .
查看答案和解析>>
科目:初中数学 来源:上海市2016-2017学年度第一学期八年级期末考试试卷 题型:解答题
如图,点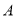 、
、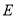 、
、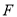 、
、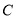 在同一直线上,
在同一直线上, 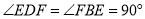 ,
, 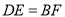 ,
, 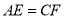 .求证
.求证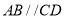 .
.
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2016-2017学年七年级下学期期末考试数学试卷 题型:单选题
下列说法正确的有( )
①近似数7.4与7.40是一样的;②近似数8.0精确到十分位;③近似数9.62精确到百分位;④由四舍五入得到的近似数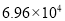 精确到百分位.
精确到百分位.
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】(1)近似数7.4与7.40的精确度不一样,所以①错误; (2)近似数8.0精确到十分位是正确的,所以②正确; (3)近似数9.62精确到百分位是正确的,所以③正确; (4)由四舍五入得到的近似数=69600,原数中最后一个有效数字6在百位,故其是精确到百位的,所以④错误; 综上所述,正确的是②③,共2个. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com