练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    在一个不透明的布袋中装有5个红球，2个白球，3个黄球，它们除了颜色外其余都相同，从袋中任意摸出一个球，是黄球的概率为_____．

    ； 【解析】由题意可得：P（任摸一个球是黄球）=. 故答案为： .
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：山东省2018届九年级上学期第二次月考数学试卷 题型：单选题

    一个圆锥的高为4cm，底面圆的半径为3cm，则这个圆锥的侧面积为（　　）

    A. 12πcm2 B. 15πcm2 C. 20πcm2 D. 30πcm2

    B 【解析】试题解析：解:圆锥的高是4,底面半径是3, 根据勾股定理得:圆锥的母线长为 则底面周长为,侧面面积 . 故选B.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年七年级数学下册（华师大版）：期末检测2 题型：填空题

    如图，在△ABC中，∠B＝90°，AB＝10.将△ABC沿着BC的方向平移至△DEF，若平移的距离是3，则图中阴影部分的面积为________．

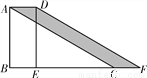
    30 【解析】【解析】 ∵直角△ABC沿BC边平移3个单位得到直角△DEF，∴AC=DF，AD=CF=3，∴四边形ACFD为平行四边形，∴S平行四边形ACFD=CF•AB=3×10=30，即阴影部分的面积为30．故答案为：30．

    查看答案和解析>>

    科目：初中数学 来源：辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型：解答题

    已知△ABC为等边三角形，点D为直线BC上的一动点（点D不与B、C重合），以AD为边作菱形ADEF（A、D、E、F按逆时针排列），使∠DAF=60°，连接CF．

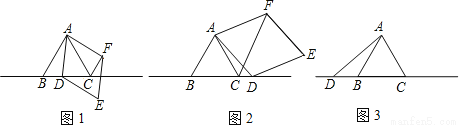
    （1）如图1，当点D在边BC上时，求证：①BD=CF；②AC=CF+CD；

    （2）如图2，当点D在边BC的延长线上且其他条件不变时，结论AC=CF+CD是否成立？若不成立，请写出AC、CF、CD之间存在的数量关系，并说明理由；

    （3）如图3，当点D在边CB的延长线上且其他条件不变时，补全图形，并直接写出AC、CF、CD之间存在的数量关系．

    （1）证明见解析；（2）AC=CF+CD不成立，AC、CF、CD之间存在的数量关系是AC=CF﹣CD；（3）补图见解析，AC=CD﹣CF． 【解析】 试题分析：（1）根据已知得出AF=AD，AB=BC=AC，∠BAC=∠DAF=60°，求出∠BAD=CAF，证△BAD≌△CAF，推出CF=BD即可； （2）求出∠BAD=∠CAF，根据SAS证△BAD≌△CAF，推出BD=CF即可...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型：填空题

    如图，在半径为3的半圆的初始状态是直径平行于桌面上的直线b，然后把半圆沿直线b进行无滑动滚动，使半圆的直径与直线b重合为止，则圆心运动路径的长度等于_____．

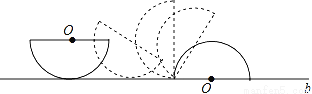
    3π； 【解析】如下图所示，由题意可知，圆心O的运动路线长=OA+， ∵OA=BC=， ， ∴圆心O运动路线长=. 故答案为： .

    查看答案和解析>>

    科目：初中数学 来源：辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型：单选题

    如图是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c＜0的解集是（　　）

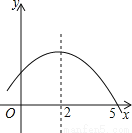
    A. -1＜x＜5 B. x＞5 C. x＜-1且x＞5 D. x＜-1或x＞5

    D 【解析】由图可知，抛物线的对称轴为直线x=2，与x轴的一个交点坐标为（5，0）， ∴函数图象与x轴的另一交点坐标为（-1，0）， ∴ax2+bx+c＜0的解集是x＜-1或x＞5． 故选C.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型：单选题

    关于x的一元二次方程x2+a2﹣1=0的一个根是0，则a的值为（　　）

    A. ﹣1 B. 1 C. 1或﹣1 D. 3

    C 【解析】由题意可得： ，解得. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2017-2018学年九年级上学期期末考试数学试卷 题型：填空题

    某果园2014年水果产量为100吨，2016年水果产量为144吨，则该果园水果产量的年平均增长率为_____．

    20% 【解析】试题分析：根据题意，得 100（1+x）2=144，解方程得x1=0.2，x2=﹣2.2．x2=﹣2.2不符合题意，舍去．故答案为20%．

    查看答案和解析>>

    科目：初中数学 来源：江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型：解答题

    已知一次函数y1＝kx＋b的图像经过点（0，-2），（2，2）.

    （1）求一次函数的表达式，并在所给直角坐标系中画出此函数的图像；；

    （2）根据图像回答：当x 时，y1=0；

    （3）求直线y1＝kx＋b、直线y2＝-2x+4与y轴围成的三角形的面积．

    （1）y＝2x-2 （2）x=1 （3） 【解析】试题分析：（1）利用待定系数法将坐标代入解析式，解方程组即可得解析式，经过给的两点即可画出函数的图象； （2）观察图象即可得； （3）求出两个函数图象的交点，两函数图象与y轴的交点，然后利用三角形面积公式即可得. 试题解析：（1）由一次函数y1＝kx＋b的图像经过点（0，-2），（2，2），则有 ，解得： ，所以解析式...

    查看答案和解析>>

    同步练习册答案