
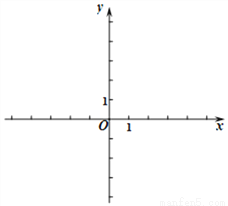
已知一次函数y1=kx+b的图像经过点(0,-2),(2,2).
(1)求一次函数的表达式,并在所给直角坐标系中画出此函数的图像;;
(2)根据图像回答:当x 时,y1=0;
(3)求直线y1=kx+b、直线y2=-2x+4与y轴围成的三角形的面积.
科目:初中数学 来源:辽宁省抚顺县2018届九年级上学期期末教学质量检测数学试卷 题型:填空题
在一个不透明的布袋中装有5个红球,2个白球,3个黄球,它们除了颜色外其余都相同,从袋中任意摸出一个球,是黄球的概率为_____.
; 【解析】由题意可得:P(任摸一个球是黄球)=. 故答案为: .查看答案和解析>>
科目:初中数学 来源:2017-2018学年福建省龙岩市上杭县城区片三校七年级(上)联考数学试卷 题型:解答题
(10分)某商场用2500元购进了A、B两种新型节能台灯共50盏,这两种台灯的进价,标价如下表所示:
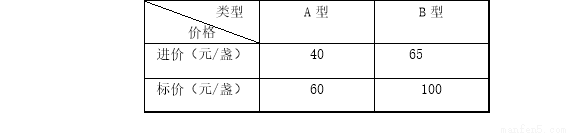
(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的九折出售,B型台灯按标价的八折出售,那么这批台灯全部售完后,商场共获利多少元?
(1)A灯30盏,B灯20盏;(2)720元. 【解析】 试题分析:(1)有两个等量关系:A型灯盏数+B型灯盏数=50,购买A型灯钱数+购买B型灯钱数=2500. (2)根据利润=售价﹣进价,知商场共获利=A型灯利润+B型灯利润. 试题解析:(1)设A型台灯购进x盏,B型台灯购进()盏. 根据题意得:,解得:,所以; 答:A型台灯购进30盏,B型台灯购进20盏....查看答案和解析>>
科目:初中数学 来源:2017-2018学年福建省龙岩市上杭县城区片三校七年级(上)联考数学试卷 题型:单选题
中国的领水面积约为370000km2,将数370000用科学记数法表示为( )
A. 37×104 B. 3.7×104 C. 0.37×106 D. 3.7×105
D 【解析】试题分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数,即370000=3.7×105. 故选:D.查看答案和解析>>
科目:初中数学 来源:江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型:解答题
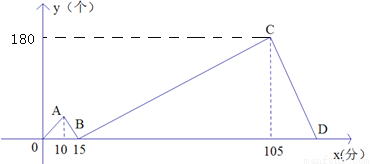
甲,乙两人同时各接受了600个零件的加工任务,甲比乙每分钟加工的数量多,两人同时开始加工,加工过程中其中一人因故障停止加工几分钟后又继续按原速加工,直到他们完成任务,如图表示甲比乙多加工的零件数量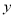 (个)与加工时间
(个)与加工时间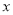 (分)之间的函数关系,观察图象解决下列问题:
(分)之间的函数关系,观察图象解决下列问题:
(1)点B的坐标是________,B点表示的实际意义是___________ _____;
(2)求线段BC对应的函数关系式和D点坐标;
(3)乙在加工的过程中,多少分钟时比甲少加工100个零件?
(4)为了使乙能与甲同时完成任务,现让丙帮乙加工,直到完成.丙每分钟能加工3个零件,并把丙加工的零件数记在乙的名下,问丙应在第多少分钟时开始帮助乙?并在图中用虚线画出丙帮助后y与x之间的函数关系的图象.
查看答案和解析>>
科目:初中数学 来源:江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型:填空题
无论a取什么实数,动点P(2a,-4a+4)总在直线l上运动,点A的坐标为(-3,0),则线段AP的最小值是______.
; 【解析】∵令a=0,则P(0,4);再令a=1,则P(2,0),由于a不论为何值此点均在直线l上, ∴设此直线的解析式为y=kx+b(k≠0), ∴ ,解得 , ∴此直线的解析式为:y=-2x+4, 易得C(2,0)、D(0,4),所以OC=2,OD=4,AB= , ∵A(-3,0),∴AC=5, 过点A作AB⊥CD于点B,则AB的长即为线段AP的最小...查看答案和解析>>
科目:初中数学 来源:江苏省附属初级中学2017-2018学年八年级1月月考数学试卷 题型:填空题
圆周率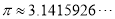 ,用四舍五入法把
,用四舍五入法把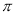 精确到千分位,得到的近似值是_______.
精确到千分位,得到的近似值是_______.
查看答案和解析>>
科目:初中数学 来源:吉林省四平市 2017-2018学年第一学期八年级数学期末综合检测卷 题型:填空题
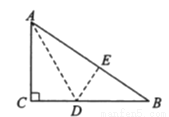
如图,有一块直角三角形纸片,两直角边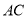 =6 cm,
=6 cm, 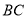 =8 cm,现将直角边
=8 cm,现将直角边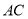 沿着直线
沿着直线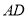 折叠,使它落在斜边
折叠,使它落在斜边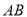 上,且与
上,且与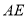 重合,则
重合,则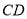 的长为___________cm.
的长为___________cm.
查看答案和解析>>
科目:初中数学 来源:山东省济南市2018届九年级1月月考数学试卷 题型:单选题
为估计池塘两岸A、B间的距离,晓明在池塘一侧选取了一点P,测得PA=16m,PB=12m,那么AB间的距离不可能是( )
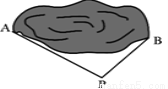
A. 5m B. 15m C. 20m D. 28m
D 【解析】【解析】 ∵PA、PB、AB能构成三角形,∴PA﹣PB<AB<PA+PB,即4m<AB<28m.故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com