
已知:如图,正比例函数y=ax的图象与反比例函数y=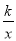 的图象交于点A(3,2)
的图象交于点A(3,2)
(1)试确定上述正比例函数和反比例函数的表达式;
(2)根据图象回答,在第一象限内,当x取何值时,反比例函数的值大于正比例函数的值?
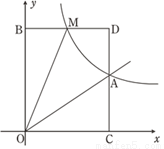
(3)点M(m,n)是反比例函数图象上的一动点,其中0<m<3,过点M作直线MB∥x轴,交y轴于点B;过点A作直线AC∥y轴交x轴于点C,交直线MB于点D.当四边形OADM的面积为6时,请判断线段BM与DM的大小关系,并说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:四川省仁寿县2017-2018学年上学期八年级期末考试数学试卷 题型:单选题
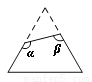
如图,一个等边三角形纸片,剪去一个角后得到一个四边形,则图中∠α+∠β的度数是( )
A. 180° B. 220° C. 240 D. 300°
C 【解析】试题分析:∵等边三角形每个内角为60°,∴两底角和=120°,又∵四边形内角和为360°,∴∠α+∠β=360°-120°=240°,故选:C.查看答案和解析>>
科目:初中数学 来源:2018届中考数学一轮复习单元检测:第7讲 一元二次方程(组)及应用 题型:单选题
广州亚运会的某纪念品原价188元,连续两次降价a%后售价为118元,下列所列方程中正确的是( )
A. 188(1+a%)2=118 B. 188(1-a%)2=118
C. 188(1-2a%)=118 D. 188(1-a2%)=118
B 【解析】当商品第一次降价a%时,其售价为168(1?a%); 当商品第二次降价a%后,其售价为168(1?a%) ·(1?a%) =168(1?a%)2. ∴168(1?a%)2=128. 故选B.查看答案和解析>>
科目:初中数学 来源:浙江杭州上城区建兰中学2018届九年级上学期期中数试卷 题型:单选题
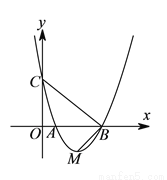
如图,抛物线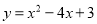 与
与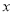 轴交于
轴交于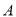 ,
, 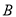 两点,与
两点,与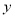 轴交于点
轴交于点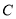 ,顶点为
,顶点为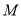 ,连结
,连结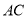 ,
, 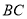 .在
.在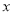 轴上是否存在点
轴上是否存在点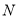 ,使以
,使以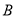 ,
, 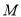 ,
, 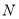 为顶点的三角形与
为顶点的三角形与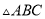 相似,则满足条件的所有
相似,则满足条件的所有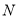 点的坐标为( )
点的坐标为( )
A. 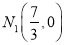 ,
, 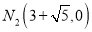 B.
B. 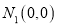 ,
, 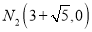
C. 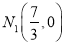 ,
, 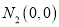 ,
, 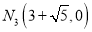 D.
D. 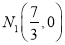 ,
, 
查看答案和解析>>
科目:初中数学 来源:浙江杭州上城区建兰中学2018届九年级上学期期中数试卷 题型:单选题
超市有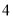 个入口和
个入口和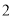 个出口,小方从进入超市到走出超市,一共有( )种不同的出入路线的可能
个出口,小方从进入超市到走出超市,一共有( )种不同的出入路线的可能
A. 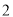 B.
B. 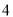 C.
C. 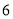 D.
D. 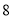
查看答案和解析>>
科目:初中数学 来源:广东省汕头市龙湖区2018届九年级上学期期末质量检测数学试卷 题型:解答题
如图,△ABC中,点D在边AB上,满足∠ACD=∠ABC,若AC=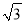 ,AD=1,求DB的长.
,AD=1,求DB的长.
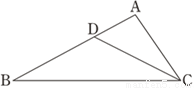
查看答案和解析>>
科目:初中数学 来源:广东省汕头市龙湖区2018届九年级上学期期末质量检测数学试卷 题型:填空题
方程x2=2x的解为____________.
x1=0,x2=2 【解析】试题分析:先移项得到x2﹣2x=0,再把方程左边进行因式分解得到x(x﹣2)=0,方程转化为两个一元一次方程:x=0或x﹣2=0,即可得到原方程的解为x1=0,x2=2. 【解析】 ∵x2﹣2x=0, ∴x(x﹣2)=0, ∴x=0或x﹣2=0, ∴x1=0,x2=2. 故答案为x1=0,x2=2.查看答案和解析>>
科目:初中数学 来源:2018届中考数学专题复习同步练习题:锐角三角函数和解直角三角形(有答案) 题型:单选题
一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度为1米,则地毯的面积至少需要( )
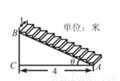
A. 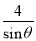 米² B.
米² B. 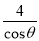 米² C. (
米² C. (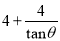 )米² D. (
)米² D. (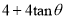 )米²
)米²
查看答案和解析>>
科目:初中数学 来源:人教版九年级下册数学 第29章 投影与视图 单元检测卷 题型:填空题
如图,某长方体的表面展开图的面积为430,其中BC=5,EF=10,则AB=________ .
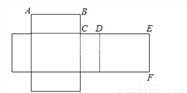
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com