
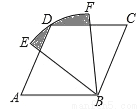
如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形EBF的半径为2,圆心角为60°,则图中阴影部分的面积是 .
科目:初中数学 来源:安徽省2018届九年级上学期第二次月考数学试卷 题型:单选题
如图,△ABC中,∠C=90°,AD是∠BAC的角平分线,交BC于点D,那么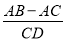 =( )
=( )
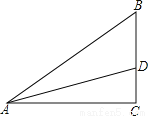
A. sin∠BAC B. cos∠BAC C. tan∠BAC D. tan∠ABC
C 【解析】试题分析:过点D作DE⊥AB于E, ∵AD是∠BAC的角平分线,DE⊥AB于E,DC⊥AC于C,∴CD=DE, ∴Rt△ADE≌Rt△ADC(HL), ∴AE=AC, ∴=tan∠BDE, ∵∠BAC=∠BDE,(同角的余角相等) ∴=tan∠BDE=tan∠BAC,故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型:解答题
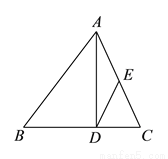
如图,在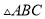 中,
中, 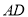 是边
是边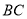 上的高,
上的高, 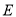 是边
是边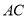 的中点,
的中点, 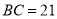 ,
, 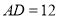 ,
, 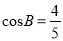 .求:(
.求:(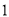 )线段
)线段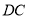 的长;(
的长;(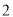 )
)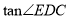 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初三上期中试卷数学试卷 题型:单选题
在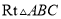 中,
中, 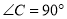 ,
, 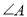 、
、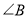 的对边是
的对边是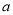 、
、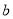 ,且满足
,且满足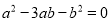 ,则
,则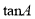 等于( ).
等于( ).
A. 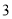 B.
B. 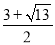 C.
C. 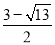 D.
D. 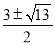
查看答案和解析>>
科目:初中数学 来源:2017年内蒙古乌兰察布市中考数学一模试卷 题型:解答题
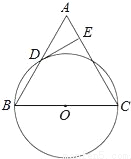
已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB=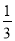 ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源:2017年内蒙古乌兰察布市中考数学一模试卷 题型:单选题
将一个半径为R,圆心角为90°的扇形围成一个圆锥的侧面(无重叠),设圆锥底面半径为r,则R与r的关系正确的是( )
A. R=8r B. R=6r C. R=4r D. R=2r
C 【解析】试题解析:根据扇形的弧长等于圆锥的底面周长,则 扇形的弧长是: 即 ∴R=4r. 故选C.查看答案和解析>>
科目:初中数学 来源:2017年江苏省徐州市中考数学模拟试卷(2) 题型:填空题
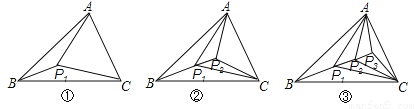
如图,△ABC的三个顶点和它内部的点P1,把△ABC分成3个互不重叠的小三角形;△ABC的三个顶点和它内部的点P1、P2,把△ABC分成5个互不重叠的小三角形;△ABC的三个顶点和它内部的点P1、P2、P3,把△ABC分成7个互不重叠的小三角形;……,△ABC的三个顶点和它内部的点P1、P2、P3……Pn,把△ABC分成 个互不重叠的小三角形.
查看答案和解析>>
科目:初中数学 来源:湖南省2017-2018学年七年级数学上期末复习检测数学试卷 题型:单选题
-2的倒数是( )
A. 2 B. -2 C. 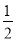 D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com