练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知，a，b，c是△ABC三边，且满|a﹣c|+|b﹣c|=0，则△ABC是_____ 三角形．

    等边 【解析】试题解析：根据非负数的性质， 解得 是等边三角形． 故答案为：等边.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：浙江省宁波市鄞州区九校2017-2018学年八年级上册数学第一次月考试卷 题型：单选题

    下列能判定三角形是等腰三角形的是（   ）

    A. 有两个角为30°、60°   B. 有两个角为40°、80°

    C. 有两个角为50°、80°   D. 有两个角为100°、120°

    C 【解析】A、因为有两个角为30°、60°,则第三个角为90°，所以此选项不正确； B、因为有两个角为40°、80°,则第三个角为60°，所以此选项不正确； C、因为有两个角为50°、80°,则第三个角为50°，有两个角相等，所以此选项正确； D、因为100°+120°>180°，所以此选项不正确； 故选：C.

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2017-2018学年八年级（上）期中数学试卷 题型：填空题

    一个多边形截去一个角后，形成新多边形的内角和为1800°，则原多边形边数为

    .

    11,12,13 【解析】 试题分析：一个多边形截去一个顶角后，新的多边形边数比原来的多边形的边数多1，设一个多边形的边数为n,则新多边形的边数为（n+1）; 一个多边形截去一个角后，形成新多边形的内角和为1800°，即

    查看答案和解析>>

    科目：初中数学 来源：湖北省黄冈市2017-2018学年八年级（上）期中数学试 题型：解答题

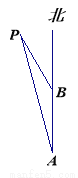
    （8分）如图，一艘轮船以15海里/时的速度，由南向北航行，在A出测得小岛P在北偏西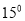方向上，两小时后，轮船在B处测得小岛P在北偏西30°方向上．在小岛周围18海里内有暗礁，若轮船

    不改变方向仍继续向前航行，问：有无触礁的危险？说明你的理由．

    见解析 【解析】 试题分析：过P作PD垂直与AB，交AB延长线于点D，在直角三角形PBD中，利用30°角所对的直角边等于斜边的一半得到PB=2PD，由PB的长求出PD的长，由PD的长与18比较大小，即可对轮船不改变方向仍继续向前航行，有无触礁的危险作出判断． 试题解析：【解析】 有危险，理由如下： 过点P作PD⊥AB，交AB的延长线与点D， 由题意可知：∠A=15°...

    查看答案和解析>>

    科目：初中数学 来源：湖北省黄冈市2017-2018学年八年级（上）期中数学试 题型：填空题

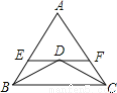
    如图，等边△ABC的边长为6，∠ABC，∠ACB的角平分线交于点D，过点D作EF∥BC，交AB、CD于点E、F，则EF的长度为___________．

    4 【解析】试题分析：根据BD和CD分别平分∠ABC和∠ACB，和EF∥BC，利用两直线平行，内错角相等和等量代换，求证出BE=DE，DF=FC．然后即可得出答案． 【解析】 ∵在△ABC中，BD和CD分别平分∠ABC和∠ACB， ∴∠EBD=∠DBC，∠FCD=∠DCB， ∵EF∥BC， ∴∠EBD=∠DBC=∠EDB，∠FCD=∠DCB=∠FDC， ∴BE...

    查看答案和解析>>

    科目：初中数学 来源：湖北省黄冈市2017-2018学年八年级（上）期中数学试 题型：单选题

    如图，已知AB=A1B，A1C=A1A2，A2D=A2A3，A3E=A3A4，∠B=20°，则∠A4=（　　）

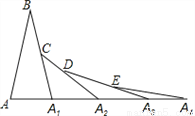
    A. 10° B. 15° C. 30° D. 40°

    A 【解析】试题分析：由∠B=20°根据三角形内角和公式可求得∠BA1A的度数，再根据等腰三角形的性质及三角形外角的性质找∠BA1A与∠A4的关系即可解答． 【解析】 ∵AB=A1B，∠B=20°， ∴∠A=∠BA1A=（180°﹣∠B）=（180°﹣20°）=80°． ∵A1C=A1A2，A2D=A2A3，A3E=A3A4， ∴∠A1CD=∠A1A2C， ∵...

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市潮南区两英镇2018届九年级上学期期末质检数学试卷 题型：解答题

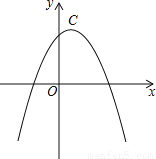
    若两条抛物线的顶点相同，则称它们为“友好抛物线”，

    抛物线C1：y1=﹣2x2+4x+2与C2：y2=﹣x2+mx+n为“友好抛物线”．

    （1）求抛物线C2的解析式．

    （2）点A是抛物线C2上在第一象限的动点，过A作AQ⊥x轴，Q为垂足，求AQ+OQ的最大值．

    （3）设抛物线C2的顶点为C，点B的坐标为（﹣1，4），问在C2的对称轴上是否存在点M，使线段MB绕点M逆时针旋转90°得到线段MB′，且点B′恰好落在抛物线C2上？若存在求出点M的坐标，不存在说明理由．

    （1）y2=﹣x2+2x+3．（2）；（3）（1，2）或（1，5） 【解析】试题分析：（1）先求得y1顶点坐标，然后依据两个抛物线的顶点坐标相同可求得m、n的值； （2）设A（a，-a2+2a+3）．则OQ=x，AQ=-a2+2a+3，然后得到OQ+AQ与a的函数关系式，最后依据配方法可求得OQ+AQ的最值； （3）连接BC，过点B′作B′D⊥CM，垂足为D．接下来证明△BCM≌△MDB...

    查看答案和解析>>

    科目：初中数学 来源：广东省汕头市潮南区两英镇2018届九年级上学期期末质检数学试卷 题型：单选题

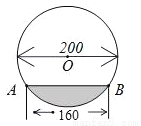
    在直径为200cm的圆柱形油槽内装入一些油以后，截面如图．若油面的宽AB=160cm，则油的最大深度为（ ）

    A. 40cm B. 60cm C. 80cm D. 100cm

    A 【解析】试题分析：连接OA，过点O作OE⊥AB，交AB于点M，由垂径定理求出AM的长，再根据勾股定理求出OM的长，进而可得出ME的长．

    查看答案和解析>>

    科目：初中数学 来源：北京市2018届九年级（上）期中数学试卷 题型：解答题

    解方程：（x﹣3）（x﹣1）=3．

    x1=0，x2=4． 【解析】 试题分析：先把方程化为一般式，然后利用因式分解法解方程． 试题解析：方程化为x2﹣4x=0，x（x﹣4）=0，所以x1=0，x2=4．

    查看答案和解析>>

    同步练习册答案