
已知m是方程3x2﹣6x﹣2=0的一根,则m2﹣2m=_____.
【解析】把x=m代入方程得:3m2﹣6m﹣2=0, 即3m2﹣6m=2,3(m2﹣2m)=2, ∴m2﹣2m=, 故答案是: . 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源:北师大版 七年级数学下册 第一章 整式的乘除 单项式与单项式相乘 专题练习题 含答案 题型:单选题
计算:2x·(-3xy)2·(-x2y)3的结果是( )
A. -12x9y5 B. -18x9y5 C. 12x9y5 D. 18x6y5
B 【解析】试题分析:同底数幂的乘法法则:底数不变,指数相加;幂的乘方法则,底数不变,指数相乘.原式=,故本题选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:填空题
如图所示是反比例函数y=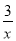 与y=-
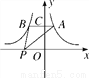
与y=-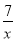 在x轴上方的图象,点C是y轴正半轴上的一点,过点C作AB∥x轴分别交这两个图象于点A,B.若点P在x轴上运动,则△ABP的面积等于________.
在x轴上方的图象,点C是y轴正半轴上的一点,过点C作AB∥x轴分别交这两个图象于点A,B.若点P在x轴上运动,则△ABP的面积等于________.
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:解答题
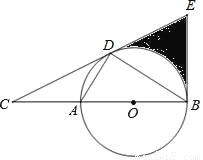
如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,CD=2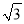 .
.
①若∠C=30°,求图中阴影部分的面积;
②若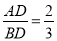 ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:解答题
解方程:x2﹣2x=0.
x1=0,x2=2 【解析】试题分析:先用因式分解法将方程变形为x(x-2)=0,求解等价方程x=0、x-2=0,即可得到原方程的解. 试题解析:x(x﹣2)=0, x=0或x﹣2=0, 所以x1=0,x2=2.查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:单选题
若点M(﹣1,y1),N(1,y2),P(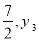 )都在抛物线y=﹣mx2+4mx+m2+1(m>0)上,则下列结论正确的是( )
)都在抛物线y=﹣mx2+4mx+m2+1(m>0)上,则下列结论正确的是( )
A. y1<y2<y3 B. y1<y3<y2 C. y3<y1<y2 D. 2<y1<y3
B 【解析】观察二次函数的图象可知:y1<y3<y2. 故选:B.查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:单选题
若2x=3y,则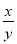 的值为( )
的值为( )
A. 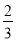 B.
B. 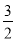 C.
C. 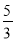 D.
D. 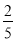
查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第一章整式乘法1.7整式的除法课时练习 题型:单选题
(4x2y4+4x2z ) ÷(2x)2等于( )
A. 4y4+z B. -y4+z C. y4+x2z D. y4+z
D 【解析】(4x2y4+4x2z ) ÷(2x)2=(4x2y4+4x2z ) ÷4x2=4x2y4÷4x2+4x2z ÷4x2= y4+x2z, 故选:D.查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 2.2 探索直线平行的条件(1) 同步练习 题型:解答题
如图所示,直线AB,CD被直线EF所截,如果∠1=70°,∠2=110°,试说明:AB//CD.
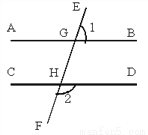
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com