
对于任何有理数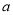 ,下列各式中一定为负数的是
,下列各式中一定为负数的是
A. 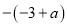 B.
B. 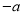 C.
C. 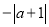 D.
D. 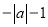
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:河南省商丘市2017-2018学年上期七年级数学期末第一次模拟检测试卷 题型:解答题
点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角形的直角三角板的直角顶点放在点O处.
(1)如图1,将三角板MON的一边ON与射线OB重合,则∠MOC=___________;
(2)如图2,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
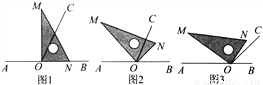
(3)将三角板MON绕点O逆时针旋转至图3时,∠NOC=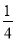 ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市盐都区2017届九年级上学期期末考试数学试卷 题型:单选题
如图所示,二次函数y=ax2+bx+c的图象中,王慧同学观察得出了下面四条信息:
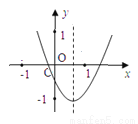
(1)b2-4ac>0;(2)c>-1;(3)2a+b<0;(4)a+b+c<0,其中正确的有 ( )
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】由图可以知道,抛物线与x轴有两个交点, ∴,故(1)正确; ∵抛物线与y轴的交点(0,c)在(0,-1)的上方, ∴c>-1,故(2)正确; ∵对称轴x=<1,且a>0, ∴-b<2a,则2a+b>0,故(3)错误; 由图象知,当x=1时,y<0,即a+b+c<0,故(4)正确; 故选C.查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
计算:
(1) 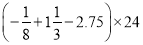 (2)
(2) 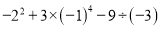
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
如果关于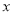 的方程
的方程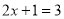 和方程
和方程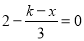 的解相同,那么
的解相同,那么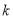 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
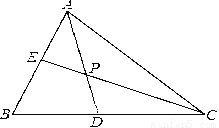
如图,△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,AD、CE相交于点P
(1) 求∠CPD的度数
(2) 若AE=3,CD=7,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
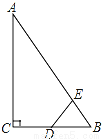
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒(0≤t<6),连接DE,当△BDE是直角三角形时,t的值为 .
查看答案和解析>>
科目:初中数学 来源:安徽省凤阳县梅市2017-2018学年九年级第一学期期末数学试卷 题型:解答题
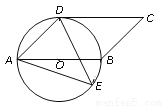
如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45?.
(1)试判断CD与⊙O的位置关系,并证明你的结论;
(2)若⊙O的半径为3,sin∠ADE=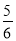 ,求AE的值.
,求AE的值.
查看答案和解析>>
科目:初中数学 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:单选题
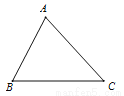
如图,△ABC中,∠A=70°,AB=4,AC= 6,将△ABC沿图中的虚线剪开,则剪下的阴影三角形与原三角形不相似的是( )
A. 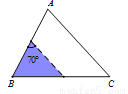 B.
B. 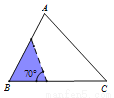
C. 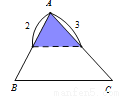 D.
D. 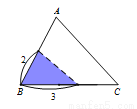
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com