
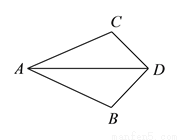
如图,在下列条件中,不能证明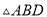 ≌
≌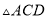 的是( ).
的是( ).
A. 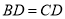 ,
, 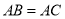 B.
B. 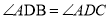 ,
, 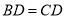
C. 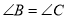 ,
, 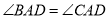 D.
D. 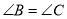 ,
, 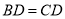
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:初中数学 来源:江苏省连云港市灌南县私立新知双语学校2018届九年级(上)期中数学模拟试卷 题型:单选题
如图,AB是⊙O的弦,AC是⊙O切线,A为切点,BC经过圆心.若∠B=20°,则∠C的大小等于( )
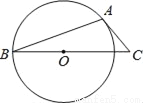
A. 20° B. 25° C. 40° D. 50°
D 【解析】试题解析:如图,连接OA, ∵AC是⊙O的切线, ∴∠OAC=90°, ∵OA=OB, ∴∠B=∠OAB=25°, ∴∠AOC=50°, ∴∠C=40°. 故选C.查看答案和解析>>
科目:初中数学 来源:浙江杭州下城区观成中学2018届九年级上学期期中数学试卷 题型:填空题
从1,2,3,4中任取两个不同的数,其乘积大于4的概率是 .
. 【解析】试题分析:首先根据题意画出树状图,然后由树状图求得所有等可能的结果与其乘积大于4的情况,再利用概率公式即可求得答案. 【解析】 画树状图得: ∵共有12种等可能的结果,任取两个不同的数,其乘积大于4的有6种情况, ∴从1、2、3、4中任取两个不同的数,其乘积大于4的概率是:=. 故答案为:.查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型:解答题
解不等式:(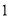 )
)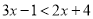 . (
. (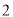 )
)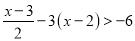 .
.
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型:单选题
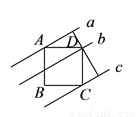
如图,四边形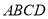 是正方形,直线
是正方形,直线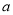 ,
, 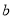 ,
, 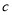 分别通过
分别通过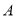 、
、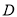 、
、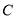 三点,且
三点,且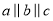 .若
.若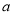 与
与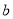 之间的距离是
之间的距离是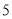 ,
, 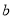 与
与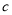 之间的距离是
之间的距离是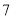 ,则正方形
,则正方形 的面积是( ).
的面积是( ).
A. 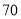 B.
B. 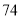 C.
C. 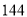 D.
D. 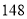
查看答案和解析>>
科目:初中数学 来源:江西省南昌市2018届九年级(上)期中数学试卷 题型:解答题
(1)如图(1),在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
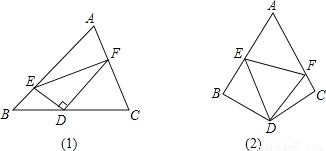
①求证:BE+CF>EF.
②若∠A=90°,探索线段BE、CF、EF之间的数量关系,并加以证明;
(2)如图(2),在四边形ABCD中,∠B+∠C=180°,DB=DC,∠BDC=120°,以D为顶点作一个60°角,角的两边分别交AB、AC于E、F两点,连接EF,探索线段BE、CF、EF之间的数量关系,并加以证明.
(1)①见解析;②BE2+CF2=EF2.证明见解析;(2)EF= EB+CF,证明见解析. 【解析】 试题分析:(1)①如图(1)延长ED到G,使DG=ED,连接CG,FG,根据条件证明△DCG≌△DBE,得DG=DE,CG=BE,易证FD垂直平分线段EG,则FG=FE,把问题转化到△CFG中,运用三边关系比较大小; ②结论:BE2+CF2=EF2.若∠A=90°,则∠B+∠C...查看答案和解析>>
科目:初中数学 来源:江西省南昌市2018届九年级(上)期中数学试卷 题型:解答题
在实数范围内定义一种新运算“#”,其规则时:a#b=a2﹣b2.
(1)求4#3与(﹣1)#(﹣2)的值;
(2)求(x+2)#5=0中的x值.
(1)7,-3;(2)x1=3或x2=﹣7. 【解析】试题分析:根据a#b=a2﹣b2,可得答案. 试题解析:【解析】 (1)4#3=42﹣32=7,(﹣1)#(﹣2)=(﹣1)2﹣(﹣2)2=﹣3; (2)由题意得:(x+2)2﹣52=0,解得x+2=±5,∴ x1=3,x2=﹣7.查看答案和解析>>
科目:初中数学 来源:河南省周口市西华县2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
下表为某市居民每月用水收费标准(单位:元/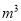 ).
).
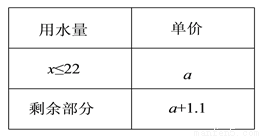
(1)某用户用水10立方米,共交水费23元,求a的值.
(2) 在(1)的前提下,该户5月份交水费71元,请问该用户用水多少立方米?
(1)a 的值为 2.3;(2)该用户用水28立方米. 【解析】试题分析:(1)直接利用10a=23进而求出即可; (2)首先判断得出x>22,进而表示出总水费,解方程即可. 试题解析:【解析】 (1)由题意可得:10a=23,解得:a=2.3. 答:a的值为2.3; (2)设用户水量为x立方米,∵用水22立方米时,水费为:22×2.3=50.6<71,∴x>22,...查看答案和解析>>
科目:初中数学 来源:山东省枣庄市2017-2018学年八年级(上)期中数学复习试卷 题型:单选题
有个数值转换器,原理如下:
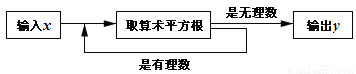
当输入的x值为16时,输出的y是( )
A. 2 B. 4 C. 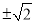 D.
D. 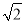
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com