
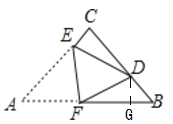
如图,在△ABC中, 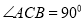 , AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则
, AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则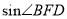 的值为_____________.
的值为_____________.
【答案】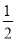
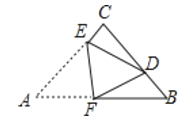
【解析】分析:过点D作DG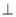 AB于点G.根据折叠性质,可得AE=DE=2,AF=DF,CE=1,
AB于点G.根据折叠性质,可得AE=DE=2,AF=DF,CE=1,
在Rt△DCE中,由勾股定理求得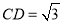 ,所以DB=
,所以DB=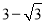 ;在Rt△ABC中,由勾股定理得
;在Rt△ABC中,由勾股定理得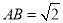 ;在Rt△DGB中,由锐角三角函数求得
;在Rt△DGB中,由锐角三角函数求得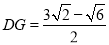 ,
, 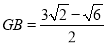 ;
;
设AF=DF=x,则FG= 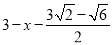 ,在Rt△DFG中,根据勾股定理得方程
,在Rt△DFG中,根据勾股定理得方程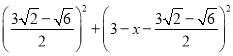 =
=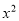 ,解得
,解得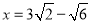 ,从而求得
,从而求得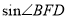 .的值
.的值
详【解析】
如图所示,过点D作DG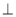 AB于点G.
AB于点G.
根据折叠性质,可知△AEF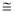 △DEF,
△DEF,
∴AE=DE=2,AF=DF,CE=AC-AE=1,
在Rt△DCE中,由勾股定理得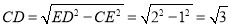 ,
,
∴DB=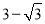 ;
;
在Rt△ABC中,由勾股定理得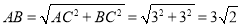 ;
;
在Rt△DGB中, 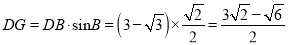 ,
, 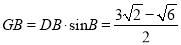 ;
;
设AF=DF=x,得FG=AB-AF-GB=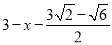 ,
,
在Rt△DFG中, 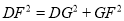 ,
,
即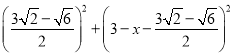 =
=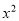 ,
,
解得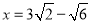 ,
,
∴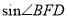 =
=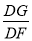 =
=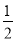 .
.
故答案为: 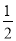 .
.
点睛:主要考查了翻折变换的性质、勾股定理、锐角三件函数的定义;解题的关键是灵活运用折叠的性质、勾股定理、锐角三角函数的定义等知识来解决问题.
【题型】填空题
【结束】
18
规定:[x]表示不大于x 的最整数,(x) 表示不小于x的最小整数,[x) 表示最接近x的整数(x≠n+0.5,n为整数),例如:[2.3]=2,(2.3)=3,[2.3)=2,则下列说法正确的是__________(写出所有正确说法).
①当x=1.7时,[x]+(x)+[x)=6;
②当x=-2.1时,[x]+(x)+[x)=-7;
③方程4[x]+3(x)+[x)=11的解为1<x<1.5;
④当-1<x<1时, 函数y=[x]+(x)+x 的图像y=4x 的图像有两个交点.
科目:初中数学 来源:江苏省无锡新吴区2017-2018学年第二学期4月初二数学期中试卷 题型:单选题
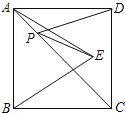
如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )
A. 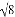 B. 3 C. 4 D. 2
B. 3 C. 4 D. 2
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市江都区邵凡片2017-2018学年八年级下学期期中考试数学试卷 题型:单选题
下列说法正确的是( )
(1)抛一枚硬币,正面一定朝上;
(2)掷一颗骰子,点数一定不大于6;
(3)为了解一种灯泡的使用寿命,宜采用普查的方法;
(4)“明天的降水概率为80%”,表示明天会有80%的地方下雨.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源:山东省济南历下区2018届一模数学试卷 题型:解答题
如图,已知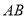 是
是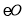 的直径,CD与
的直径,CD与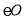 相切于C,
相切于C, 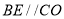 .
.
(1)求证:BC 是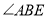 的平分线.
的平分线.
(2)若DC=8, 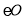 的半径OA=6,求CE的长.
的半径OA=6,求CE的长.
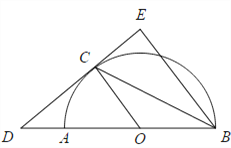
【答案】(1)证明见解析;(2)4.8
【解析】分析:(1)由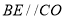 ,推出
,推出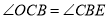 ,由
,由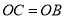 ,推出
,推出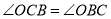 ,可得
,可得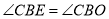 .(2)在
.(2)在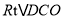 中,求出OD,由
中,求出OD,由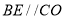 ,可得
,可得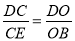 ,由此即可解决问题.
,由此即可解决问题.
详【解析】
(1)证明:因为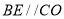 ,
,
所以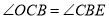 ,
,
又因为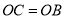 ,
,
所以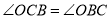 ,
,
故可得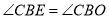 ,
,
即可得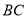 是
是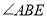 的平分线.
的平分线.
(2)因为DE是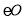 的切线,
的切线,
所以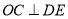 ,即在
,即在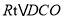 中,DC=8,OC=OA=6,所以
中,DC=8,OC=OA=6,所以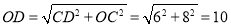 ,
,
又因为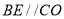 ,
,
所以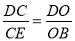 ,
,
所以 ,
,
即可得EC=4.8
点睛:本题主要考查了切线的性质及相似三角形的应用,题目难度适中,会综合运用所考查的知识点是解题的关键.
【题型】解答题
【结束】
23
“食品安全”受到全社会的广泛关注,济南市某中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两份尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题.
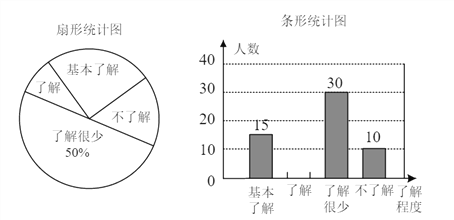
(1)接受问卷调查的学生共有_____人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_____ .
(2)请补全条形统计图.
(3)若该中学共有学生900人,请根据上述调查结果,估计该中学学生中对食品安全知识达到“了解”和“基本了解”程度的总人数.
(4)若从对食品安全知识达到“了解”程度的2个女生和2个男生中随机抽取2人参加食品安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
查看答案和解析>>
科目:初中数学 来源:北京市2018届初三数学中考复习 综合练习题 含答案 题型:解答题
如图,在△ABC中,∠C=90°,D,F是AB边上的两点,以DF为直径的⊙O与BC相交于点E,连接EF,过F作FG⊥BC于点G,其中∠OFE= ∠A.
∠A.
(1)求证:BC是⊙O的切线;
(2)若sinB= ,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).
,⊙O的半径为r,求△EHG的面积(用含r的代数式表示).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com