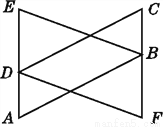
如图,已知A,D,E三点共线,C,B,F三点共线,AB=CD,AD=CB,DE=BF,那么BE与DF之间有什么数量关系?请说明理由. 答案见解析 [解析]试题分析: 连接BD.由SSS可证明△ABD≌△CDB.从而得到∠A=∠C.再由AD=CB.DE=BF.得到AE=CF.即可证明△ABE≌△CDF.由全等三角形的性质即可得出结论．试题解析:[解析] BE=D 题目和参考答案——青夏教育精英家教网—

如图,已知A,D,E三点共线,C,B,F三点共线,AB=CD,AD=CB,DE=BF,那么BE与DF之间有什么数量关系?请说明理由.

答案见解析【解析】试题分析：连接BD，由SSS可证明△ABD≌△CDB，从而得到∠A=∠C，再由AD=CB，DE=BF，得到AE=CF，即可证明△ABE≌△CDF，由全等三角形的性质即可得出结论．试题解析：【解析】 BE=DF．理由如下：如图，连接BD．在△ABD和△CDB中， ∵AB=CD，AD=CB，BD=DB，∴△ABD≌△CDB(SSS)，∴∠A=∠C．...

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：北师大版七年级数学下2.1.2 垂线的定义与性质同步练习 题型：单选题

下列说法正确的有(　　)

①在同一平面内,过直线上一点有且只有一条直线垂直于已知直线;

②在同一平面内,过直线外一点有且只有一条直线垂直于已知直线;

③在同一平面内,过一点可以画一条直线垂直于已知直线;

④在同一平面内,有且只有一条直线垂直于已知直线.

A. 1个 B. 2个 C. 3个 D. 4个

C 【解析】试题解析：由垂线的性质可知①②③正确. 故选C.

查看答案和解析>>

科目：初中数学 来源：北师大版七年级下册第一章　整式的乘除单元测试卷 题型：填空题

已知P=3xy－8x＋1，Q=x－2xy－2，当x≠0时，3P－2Q=7恒成立，则y的值为__.

2 【解析】∵P=3xy?8x+1，Q=x?2xy?2， ∴3P?2Q=3(3xy?8x+1)?2(x?2xy?2)=7恒成立， ∴9xy?24x+3?2x+4xy+4=7， 13xy?26x=0， 13x(y?2)=0， ∵x≠0， ∴y?2=0， ∴y=2；故答案为：2.

查看答案和解析>>

科目：初中数学 来源：北师大版七年级数学下3.2 用关系式表示的变量间关系同步练习 题型：填空题

如图,梯形的上底长是5 cm,下底长是11 cm.当梯形的高由大变小时,梯形的面积也随之发生变化.

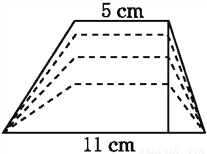
(1)在这个变化过程中,自变量是____________,因变量是____________;

(2)梯形的面积y(cm2)与高x(cm)之间的关系式为____________;

(3)当梯形的高由10 cm变化到1 cm时,梯形的面积由____________变化到____________.

梯形的高梯形的面积 y=8x 80cm2 8cm2 【解析】（1）由题意可知：在上述变化过程中，自变量是“梯形的高”；因变量是“梯形的面积”；（2）梯形的面积y(cm2)与高x(cm)之间的关系式为：；（3）∵当梯形的高时，梯形的面积（cm2），当梯形的高时，梯形的面积（cm2）， ∴当梯形的高由10cm变化到1cm时，梯形的面积由80cm2变化到8cm2....

查看答案和解析>>

科目：初中数学 来源：北师大版七年级数学下3.2 用关系式表示的变量间关系同步练习 题型：单选题

一个长方形的周长为30,则长方形的面积y与长方形一边长x的关系式为(　　)

A. y=x(15-x) B. y=x(30-x) C. y=x(30-2x) D. y=x(15+x)

A 【解析】∵长方形的周长为30，其中一边长为， ∴该长方形的另一边长为：， ∴该长方形的面积： . 故选A.

查看答案和解析>>

科目：初中数学 来源：北师大版七年级数学下4.3.3 用“边角边”判定三角形全等同步练习 题型：解答题

如图,已知AB=CD,BC=DA,E,F是AC上的两点,且AE=CF.试说明:BF=DE.

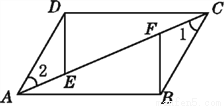
答案见解析【解析】试题分析：先利用“SSS”证明△ABC≌△CAD，得到∠1=∠2，然后根据“SAS”可判断△BCF≌△DAE，即可得出结论．试题解析：【解析】在△ABC和△CDA中，∵AB=CD，BC=DA，CA=AC，∴△ABC≌△CDA(SSS)，∴∠1=∠2(全等三角形的对应角相等)．在△BCF和△DAE中，∵BC=DA，∠1=∠2，CF=AE，∴△BCF≌△D...

查看答案和解析>>

科目：初中数学 来源：北师大版七年级数学下4.3.3 用“边角边”判定三角形全等同步练习 题型：单选题

如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（）

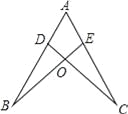
A. ∠B=∠C B. AD=AE C. BD=CE D. BE=CD

D 【解析】试题分析：添加A可以利用ASA来进行全等判定；添加B可以利用SAS来进行判定；添加D选项可以得出AD=AE，然后利用SAS来进行全等判定.

查看答案和解析>>

科目：初中数学 来源：北师大版数学七年级下册第四章4.4用尺规作三角形课时练习 题型：解答题

求作等腰三角形，使它的底边和底边上的高等于同一条已知线段。

作图见解析【解析】分析：∵底边和底边上的高等于同一条已知线段∴先作底边，再作高； ∵求作的是一个等腰三角形∴底边上的高在这条底的中垂线上∴需要作底边的中垂线. 本题解析：已知：线段A 求作：△ABC，使AB=AC，BC=A，BC上的高AD=A 作法：（1）作线段BC=A （2）作线段BC的垂直平分线MN，MN交BC于D （3）在MN上截取DA=A...

查看答案和解析>>

科目：初中数学 来源：北师大版七年级数学下4.3.1 用“边边边”判定三角形全等同步练习 题型：解答题

如图,已知线段AB,CD相交于点O,AD,CB的延长线交于点E,OA=OC,EA=EC.

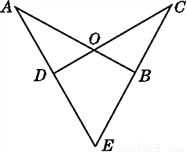
(1)试说明:∠A=∠C;

(2)在(1)的解答过程中,需要作辅助线,它的意图是什么?

（1）见解析；（2）构造全等三角形. 【解析】分析：（1）根据题意，没有证明两三角形全等的条件，所以要作条辅助线，连接OE；然后就可以利用SSS全等判定定理证明两三角形全等，继而∠A=∠C，本题即可证明（1），（2），说明OE的意义即可. 本题解析： (1)如图,连接OE. 在△EAO和△ECO中, 所以△EAO≌△ECO(SSS). 所以∠A=∠C(全等三角形...

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学