
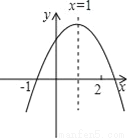
已知二次函数y=ax2+bx+c的图象如图所示,有下列结论:①abc<0;②a+c>b;③3a+c<0;④a+b>m(am+b)(其中m≠1),其中正确的结论有_____.
科目:初中数学 来源:江西省九江市彭泽县2017-2018学年七年级(上)期中数学试卷(解析版) 题型:填空题
观察下列算式:32=9,33=27,34=81,35=243,…,那么32016的末位数字为_____.
1 【解析】试题解析:已知末位数字为3, 末位数字为9, 末位数字为7, 末位数字为1, 末位数字为3, 末位数字为9, 末位数字为7, 末位数字为1, … 由此得到:3的1,2,3,4,5,6,7,8,…次幂的末位数字以3、9、7、1四个数字为一循环, 又∵2016÷4=504, 的末位数字与的末位数字相同是1. 故答...查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(B卷) 题型:解答题
先化简,再求值: 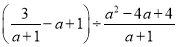 ,其中
,其中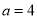 .
.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(B卷) 题型:单选题
在△ABC与△A′B′C′中,已知∠A=∠A′,AC=A′C′,下列说法错误的是( )
A. 若添加条件AB=A′B′,则△ABC与△A′B′C′全等
B. 若添加条件∠C=∠C′,则△ABC与△A′B′C′全等
C. 若添加条件∠B=∠B′,则△ABC与△A′B′C′全等
D. 若添加条件BC=B′C′,则△ABC与△A′B′C′全等
D 【解析】试题解析:A、若添加条件AB=A′B′,可利用SAS判定△ABC≌△A′B′C′,故此选项不合题意; B、若添加条件∠C=∠C′,可利用ASA判定△ABC≌△A′B′C′,故此选项不合题意; C、若添加条件∠B=∠B′,可利用AAS判定△ABC≌△A′B′C′,故此选项不合题意; D、若添加条件BC=B′C′,不能判定△△ABC≌△A′B′C′,故此选项合题意;...查看答案和解析>>
科目:初中数学 来源:四川省广元市苍溪县东溪片区2018届九年级(上)期中数学试卷 题型:解答题
已知关于x的方程k2x2﹣2(k+1)x+1=0有两个实数根.
(1)求k的取值范围;
(2)当k=1时,设所给方程的两个根分别为x1和x2,求(x1﹣2)(x2﹣2)的值.
(1)k≥﹣且k≠0;(2)﹣3. 【解析】试题分析:(1)根据根的判别式得出k的取值范围即可; (2)把k=1代入即可得出方程,根据根与系数的关系得出x1+x2,x1x2,再代入计算即可. 试题解析: (1)根据题意得k2≠0且△=4(k+1)2﹣4k2≥0, 解得k≥﹣且k≠0; (2)k=1时方程化为x2﹣4x+1=0,则x1+x2=4,x1•x2=1, ...查看答案和解析>>
科目:初中数学 来源:四川省广元市苍溪县东溪片区2018届九年级(上)期中数学试卷 题型:单选题
如图,由三个边长分别为6,9和x的正方形所组成的图形,若直线AB将它分成面积相等的两部分,则x的值是( )
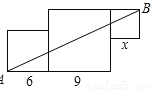
A. 1或9 B. 3或5
C. 4或6 D. 3或6
D 【解析】以AB为对角线将图形补成长方形,由已知可得缺失的两部分面积相同,即3×6=x×(9-x),解得x=3或x=6,故选D.查看答案和解析>>
科目:初中数学 来源:四川省广元市苍溪县东溪片区2018届九年级(上)期中数学试卷 题型:单选题
解方程(x+1)2=3(1+x)的最佳方法是( )
A. 直接开平方法 B. 配方法 C. 公式法 D. 因式分解法
D 【解析】(x+1)2=3(1+x), (x+1)2﹣3(1+x)=0, (x+1)(x+1﹣3)=0, 即最好的方法是因式分解法, 故选D.查看答案和解析>>
科目:初中数学 来源:四川江油小溪坝中学2017年秋七年级数学第三学月检测题 题型:单选题
如图,有一个正方体纸盒,在它的三个侧面分别画有三角形、正方形和圆,现用一把剪刀沿着它的棱剪开成一个平面图形,则展开图可以是( )
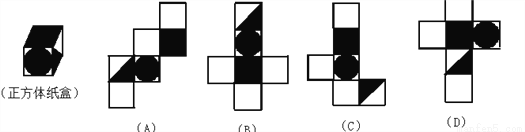
A. (A) B. (B) C. (C) D. (D)
C 【解析】对于选项A,当圆为正面时,三角形是左侧面,结合所给图示可知错误; 对于选项B,当圆为正面时,正方形为底面,结合所给图示可知错误; 对于选项C,当圆为正面时,三角形是右侧面,正方形为上底面,结合所给图示可知正确; 对于选项D,当圆为正面时,正方形是左侧面,结合所给图示可知错误. 故选C.查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年八年级上期末模拟数学试卷 题型:解答题
某公司招聘职员,对甲、乙两位候选人进行了面试和笔试,面试中包括形体和口才,笔试中包括专业水平和创新能力考察,他们的成绩(百分制)如下表:
候选人 | 面试 | 笔试 | ||
形体 | 口才 | 专业水平 | 创新能力 | |
甲 | 86 | 90 | 96 | 92 |
乙 | 92 | 88 | 95 | 93 |
若公司根据经营性质和岗位要求认为:形体、口才、专业水平、创新能力按照5:5:4:6的比确定,请计算甲、乙两人各自的平均成绩,看看谁将被录取?
从平均成绩看,应该录取乙. 【解析】试题分析:按照权重分别为5:5:4:6计算两人的平均成绩,平均成绩高将被录取. 试题解析:形体、口才、专业水平创新能力按照5:5:4:6的比确定, 则甲的平均成绩为=90.8, 乙的平均成绩为=91.9, 显然乙的成绩比甲的高,从平均成绩看,应该录取乙.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com