
解方程: 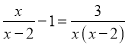 .
.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:填空题
矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
3或6 【解析】试题分析: 由题意可知有两种情况,见图1与图2; 图1:当点F在对角线AC上时,∠EFC=90°, ∵∠AFE=∠B=90°,∠EFC=90°, ∴点A、F、C共线, ∵矩形ABCD的边AD=8, ∴BC=AD=8, 在Rt△ABC中,AC==10, 设BE=x,则CE=BC﹣BE=8﹣x, 由翻折的性质得,AF=AB=6...查看答案和解析>>
科目:初中数学 来源:广东省2018届九年级上学期学业检测(二)数学试卷 题型:单选题
下列图形中是中心对称图形的有( )个.
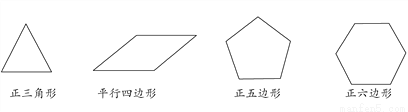
A. 1 B. 2 C. 3 D. 4
B 【解析】∵正三角形是轴对称能图形;平行四边形是中心对称图形;正五边形是轴对称图形;正六边形既是中心对称图形又是轴对称图形, ∴中心对称图形的有2个. 故选B.查看答案和解析>>
科目:初中数学 来源:湖北省孝感市八校联谊2017-2018学年九年级上册数学12月联考试卷 题型:单选题
如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为( )
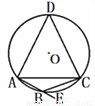
A. 130° B. 100° C. 65° D. 50°
C 【解析】∵∠CBE=50°,四边形ABCD是⊙O的内接四边形, ∴∠ADC=∠CBE=50°(圆内接四边形的一个外角等于内对角), ∵DA=DC, ∴∠DAC=∠DCA=. 故选C.查看答案和解析>>
科目:初中数学 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:解答题
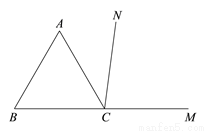
如图,CN是等边△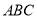 的外角
的外角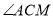 内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
(1)依题意补全图形;
(2)若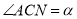 ,求
,求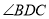 的大小(用含
的大小(用含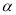 的式子表示);
的式子表示);
(3)用等式表示线段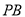 ,
, 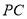 与
与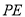 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:填空题
如图,在平面直角坐标系xOy中,△DEF可以看作是△ABC经过若干次的图形变化(轴对称、平移)得到的,写出一种由△ABC得到△DEF的过程:____________.

查看答案和解析>>
科目:初中数学 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:单选题
若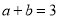 ,则
,则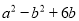 的值为( )
的值为( )
A. 3 B. 6 C. 9 D. 12
C 【解析】∵a+b=3, ∴a2-b2+6b=(a+b)(a-b)+6b=3(a-b)+6b=3a-3b+6b=3a+3b=3(a+b)=9, 故选C.查看答案和解析>>
科目:初中数学 来源:北京市海淀区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
计算:(1)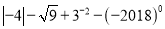 ;
;
(2)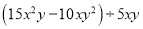 .
.
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级12月月考数学试卷 题型:单选题
一个正方体的每个面都写有一个汉字,其平面展开图如图所示,则在该正方体中,和“崇”相对的面上写的汉字是( )
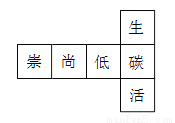
A. 低 B. 碳 C. 生 D. 活
A 【解析】空间想象或者亲手制作上图,可知选A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com