练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

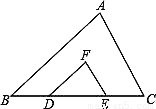
    如图，点D，E在BC上，且FD∥AB，FE∥AC．求证：△ABC∽△FDE．

    证明见解析. 【解析】 试题分析：由FD∥AB，FE∥AC，可知∠B=∠FDE，∠C=∠FED，根据三角形相似的判定定理可知：△ABC∽△FDE． 试题解析：∵FD∥AB，FE∥AC， ∴∠B=∠FDE，∠C=∠FED， ∴△ABC∽△FDE．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年吉林省中考数学一诊试卷 题型：填空题

    如图，某办公大楼正前方有一根高度是15米的旗杆ED，从办公楼顶端A测得旗杆顶端E的俯角α是45°，旗杆底端D到大楼前梯坎底边的距离DC是20米，梯坎坡长BC是12米，梯坎坡度i=1∶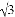，求大楼AB的高度是多少？（结果保留根号）

    29+6 【解析】试题分析:延长AB交DC于H,作EG⊥AB于G,则GH=DE=15米,EG=DH,设BH=x米,则CH=米,在直角三角形BCH中,BC=12米,由勾股定理得出方程,解方程求出BH=6米,CH=6,得出BG,EG的长度,证明三角形AEG是等腰直角三角形,得出AG=EG=6+20(米),即可得出大楼AB的高度. 试题解析: 延长AB交DC于H,作EG⊥AB于G,如图所示:...

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷（7） 题型：解答题

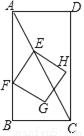
    如图，在矩形ABCD中，AB=4，BC=2，点E从点A出发，以每秒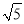个单位长度的速度沿对角线AC向终点C运动，点F从点B出发，以每秒2个单位长度的速度沿边BA向终点A运动，连结EF，将线段EF绕点F顺时针旋转90°得到线段FG，以EF，FG为边作正方形EFGH，设点E运动的时间为t秒（t＞0）．

    （1）用含t的代数式表示点E到边AB的距离．

    （2）当点G落在边AB上时，求t的值．

    （3）连结BG，设△BFG的面积为S平方单位（S＞0），求S与t之间的函数关系式．

    （4）直接写出当正方形EFGH的顶点与点B，D距离相等时的t值．

    （1）点E到边AB的距离为t（2）t=1（3）S= （4）当正方形EFGH的顶点与点B，D距离相等时的t值为s或1s或s 【解析】试题分析：（1）如图1中，作EM⊥AB于M．由EM∥BC，可得，即，延长即可解决问题； （2）如图2中，G在AB边时，由AF+FB=4，可得2t+2t=4，解方程即可； （3）分两种情形①如图3中，当0

    查看答案和解析>>

    科目：初中数学 来源：2017年吉林省长春市中考数学模拟试卷（7） 题型：单选题

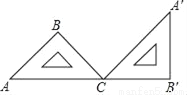
    如图，将等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置，使点A，C，B′在同一条直线上，则旋转角的大小为（　　）

    A. 45° B. 90° C. 120° D. 135°

    D 【解析】∵△ABC为等腰直角三角形， ∴∠A=∠ACB=45°， ∴∠BCB′=180°?45°=135°， ∵等腰直角三角尺ABC绕着点C顺时针旋转到A′B′C的位置， ∴∠BCB′等于旋转角， 即旋转角为135°. 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级12月月考数学试卷 题型：解答题

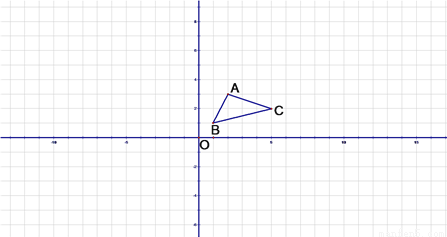
    如图,A(2,3),B(1,1),C(5,2)以原点O为位似中心,相似比为2, 将△ABC进行变换,画出变换后的图形,并求出相应的坐标.

    图形见解析 【解析】若位似比是k，则原图形上的点（x，y），经过位似变化得到的对应点的坐标是（kx，ky）或（-kx，-ky），即可得出A、B、C的对应点的坐标，顺序连接各点即可画出变换出的图形. 【解析】 ∵A(2,3)以原点O为位似中心,相似比为2,将△ABC放大， ∴A的对应点的坐标是(4,6)或(?4,?6) ， B的对应点的坐标是(2,2)或(?2,?2) ， ...

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级12月月考数学试卷 题型：填空题

    若x1=﹣1是关于x的方程x2+mx﹣5=0的一个根，则方程的另一个根x2=__．

    5 【解析】试题分析：首先将x=－1代入方程求出m的值，然后再去解关于x的一元二次方程．

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级12月月考数学试卷 题型：单选题

    在△ABC中，AB＝AC＝3，BC＝2，则6cosB等于 （ ）

    A. 3 B. 2 C. 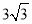D.

    B 【解析】作BC边上的高，利用等腰三角形的性质得BD的长，再利用三角函数定义求解． 【解析】 过点A作AD⊥BC于D. ∵在△ABC中，AB=AC=3，BC=2， ∴BD=DC=1.cosB==， ∴6cosB=6×=2. 故选B.

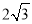
    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市汉阳区2018届九年级（上）期中数学试卷（解析版） 题型：填空题

    将抛物线y=﹣x2向右平移3个单位后所得抛物线解析式的一般式为_____．

    y=﹣（x﹣3）2． 【解析】抛物线y=﹣x2向右平移3个单位后y=﹣（x﹣3）2． 故答案为y=﹣（x﹣3）2．

    查看答案和解析>>

    科目：初中数学 来源：2017年海南省海口市中考数学模拟试卷 题型：解答题

    如图，某办公楼AB的后面有一建筑物CD，当光线与地面的夹角是22°时，办公楼在建筑物的墙上留下高2米的影子CE，而当光线与地面夹角是45°时，办公楼顶A在地面上的影子F与墙角C有25米的距离（B，F，C在一条直线上）．

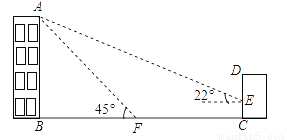
    （1）求办公楼AB的高度；

    （2）若要在A，E之间挂一些彩旗，请你求出A，E之间的距离．

    （参考数据：sin22°≈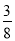，cos22°≈ 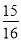，tan22°≈）

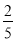    （1）教学楼的高20m；（2）A、E之间的距离约为48m． 【解析】（1）过点E作EM⊥AB于点M，设AB=x，在Rt△ABF中，由∠AFB=45°可知BF=AB=x， 在Rt△AEM中，利用锐角三角函数的定义求出x的值即可；（2）在Rt△AME中，根据cos22°=可得出结论． 【解析】 （1）过点E作EM⊥AB于点M，设AB=x， 在Rt△ABF中，∵∠AFB=45°...

    查看答案和解析>>

    同步练习册答案