
O为平面直角坐标系原点,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)求直线AB的函数表达式.
(2)若直线AB上有一动点C,且S△BOC=2,求点C的坐标.
(1)y=2x﹣2;(2)(2,2)或(-2,-6) 【解析】试题分析:(1)根据待定系数法得出解析式即可; (2)设C点坐标,根据三角形面积公式解答即可. 试题解析:【解析】 (1)设直线解析式为y=kx+b,可得: ,解得: ,直线解析式为:y=2x﹣2; (2)设C点坐标为(x,2x﹣2),∵S△BOC=2,∴ ×2×|x|=2,解得x=±2,点C的坐标为(2,2)...科目:初中数学 来源:2017年吉林省中考数学六模试卷 题型:解答题
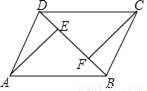
如图,在四边形ABCD中,AD=BC,BE=DF,AE⊥BD,CF⊥BD,垂足分别为E、F,求证:四边形AFCE是平行四边形.
查看答案和解析>>
科目:初中数学 来源:江苏省盐城市盐都区2016-2017学年八年级上学期期末联考数学试卷 题型:单选题
下列大学的校徽图案是轴对称图形的是( )

A.清华大学 B.北京大学 C.中国人民大学 D.浙江大学
B. 【解析】 试题分析:A.不是轴对称图形,故错误; B.是轴对称图形,故正确; C.不是轴对称图形,故错误; D.不是轴对称图形,故错误. 故选B.查看答案和解析>>
科目:初中数学 来源:黑龙江省2017-2018学年度上学期人教版七年级数学上册期末复习练习题 题型:单选题
如果线段AB=7cm,BC=5cm,且点A,B,C在同一条直线上,那么A,C两点间的距离是( )
A. 1 2cm B. 2cm C. 12cm或2cm D. 无法确定
C 【解析】【解析】 当点C在线段AB的延长线上时,如图,AC=AB+BC=7+5=12(cm),即A、C间的距离为12cm; 当点C在线段AB的上时,如图,AC=AB﹣BC=7﹣5=2(cm),即A、C间的距离为2cm. 故A、C间的距离是12cm或者2cm.故选C.查看答案和解析>>
科目:初中数学 来源:黑龙江省2017-2018学年度上学期人教版七年级数学上册期末复习练习题 题型:单选题
下列表示数a、b的点在数轴上的位置如图所示,若a>b>0,则其中正确的是( )
A. 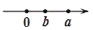 B.
B. 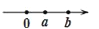
C. 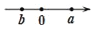 D.
D. 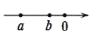
查看答案和解析>>
科目:初中数学 来源:浙江省义乌市四校2017-2018学年八年级上学期第三次作业检测(1月)数学试卷 题型:填空题
在△ABC中,AB=13,AC=20,BC边上的高为12,则△ABC的面积为_____.
126或66 【解析】试题分析:当∠B为锐角时(如图1),在Rt△ABD中,BD==5cm,在Rt△ADC中,CD==16cm,因此可知BC=21,所以可求=×21×12=126;当∠B为钝角时(如图2),在Rt△ABD中,BD==5cm,在Rt△ADC中,CD==16cm,BC=CD-BD=11cm,所以可求=×11×12=66.查看答案和解析>>
科目:初中数学 来源:浙江省义乌市四校2017-2018学年八年级上学期第三次作业检测(1月)数学试卷 题型:单选题
已知等腰三角形的周长是10,底边长y是腰长x的函数,则下列图象中,能正确反映y与x之间函数关系的图象是( )
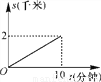
A. 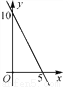 B.
B. 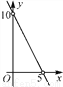 C.
C. 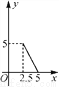 D
D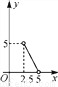
查看答案和解析>>
科目:初中数学 来源:内蒙古2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
分解因式: 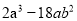 =___________.
=___________.
查看答案和解析>>
科目:初中数学 来源:江苏省南通市2017-2018学年八年级上学期第三次月考数学试卷 题型:单选题
要使式子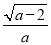 有意义,a的取值范围是 ( )
有意义,a的取值范围是 ( )
A. a≠0 B. a>-2且a≠0 C. a>-2或a≠0 D. a≥-2 且a≠0
D 【解析】试题解析:根据题意,得 解得a≥-2且a≠0. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com