
科目:初中数学 来源:人教版七年级下册数学第7-10章综合测试卷 题型:填空题
方程组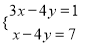 的解是 ________.
的解是 ________.
查看答案和解析>>
科目:初中数学 来源:北师大版数学九年级下册 1.1 锐角三角函数 题型:解答题
如图,在Rt△ACB中,∠ACB=90°,CD为AB边上的高,BD=3,AD=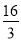 ,求sinA,cosA,tanA的值.
,求sinA,cosA,tanA的值.
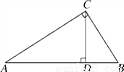
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2018届九年级上学期期中数学试卷 题型:填空题
我们规定:一个正 边形(
边形(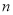 为整数
为整数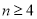 )的最短对角线与最长对角线长度的比值叫做这个正
)的最短对角线与最长对角线长度的比值叫做这个正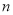 边形的“特征值”,记为
边形的“特征值”,记为 ,那么
,那么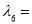 __________.
__________.
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2018届九年级上学期期中数学试卷 题型:单选题
已知函数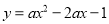 (
( 是常数,
是常数, 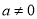 ),下列结论正确的是( ).
),下列结论正确的是( ).
A. 当 时,函数图象经过点
时,函数图象经过点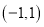 B. 当
B. 当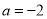 时,函数图象与
时,函数图象与 轴有两个交点
轴有两个交点
C. 若 ,函数图象顶点始终在
,函数图象顶点始终在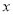 轴的下方 D. 若
轴的下方 D. 若 ,当
,当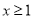 时,
时,  随
随 的增大而减小
的增大而减小
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:填空题
比较大小:sin24°________ cos66°,cos15°________ tan55°.
= < 【解析】【解析】 cos66°=sin(90°﹣66°)=sin24°,cos15°<cos0°=1,1=tan45°<tan55°,cos15°<1<tan55°.故答案为:=,<.查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:填空题
某水库水坝的坝高为10米,迎水坡的坡度为1:2.4,则该水库迎水坡的长度为________ 米.
26 【解析】【解析】 ∵大坝高10米,背水坝的坡度为1:2.4,∴水平距离=10×2.4=24(米). 根据勾股定理,可得背水面的坡长为: =26(米).故答案为:26.查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第五章 生活中的轴对称 单元检测卷 题型:填空题
如图,已知∠AOB=45°,∠AOB内有一点P,OP=6 ,M为射线OA上一动点,N为射线OB上一动点,则PM+MN+PN的最小值为________.
,M为射线OA上一动点,N为射线OB上一动点,则PM+MN+PN的最小值为________.

查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册 同步测试 1.2 幂的乘法与积的乘方 题型:单选题
下列计算正确的是( )
A. x4•x4=x16 B. (a3)2=a5 C. (ab2)3=ab6 D. a+2a=3a
D 【解析】试题分析:根据同底数幂的乘法、积的乘方与幂的乘方及合并同类项的运算法则进行计算即可得出正确答案. 试题解析:A.x4•x4=x4+4=x8≠x16,故该选项错误; B.(a3)2=a3×2=a6≠a5,故该选项错误; C.(ab2)3=a3b6≠ab6,故该选项错误; D.a+2a=(1+2)a=3a,故该选项正确; 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com