
某水库水坝的坝高为10米,迎水坡的坡度为1:2.4,则该水库迎水坡的长度为________ 米.
26 【解析】【解析】 ∵大坝高10米,背水坝的坡度为1:2.4,∴水平距离=10×2.4=24(米). 根据勾股定理,可得背水面的坡长为: =26(米).故答案为:26. 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源:人教版七年级下册数学第7-10章综合测试卷 题型:单选题
两人练习跑步,如果乙先跑16米,甲8秒可追上乙,如果乙先跑2秒钟,则甲4秒可追上乙,求甲乙二人每秒各跑多少米?若设甲每秒跑x米,乙每秒跑y米,则所列方程组应该是( )。
A.  B.
B. 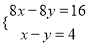 C.
C. 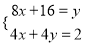 D.
D. 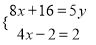
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2018届九年级上学期期中数学试卷 题型:解答题
已知:如图,  中,
中, 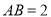 ,
, 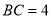 ,
, 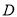 为
为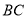 边上一点,
边上一点, 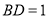 .
.

(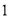 )求证:
)求证: 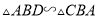 .
.
(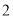 )若
)若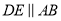 交
交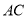 于点
于点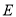 ,请再写出另一个与
,请再写出另一个与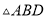 相似的三角形,并直接写出
相似的三角形,并直接写出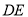 长.
长.
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2018届九年级上学期期中数学试卷 题型:单选题
抛物线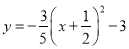 的顶点坐标是( ).
的顶点坐标是( ).
A. 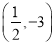 B.
B. 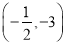 C.
C. 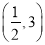 D.
D. 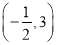
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:填空题
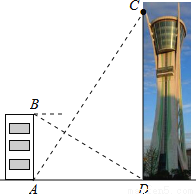
观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:单选题
某山的山顶B处有一个观光塔,已知该山的山坡面与水平面的夹角∠BDC为30°,山高BC为100米,点E距山脚D处150米,在点E处测得观光塔顶端A的仰角为60°,则观光塔AB的高度是( )
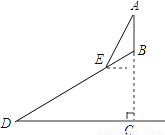
A. 50米 B. 100米 C. 125米 D. 150米
A 【解析】试题解析:作EF⊥AC于F,EG⊥DC于G, 在Rt△DEG中,EG=DE=75米, ∴BF=BC-CF=BC-CE=100-75=25(米), EF==25, ∵∠AEF=60°, ∴∠A=30°, ∴AF==75(米), ∴AB=AF-BF=50(米), 故观光塔AB的高度为50米. 故选A.查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第五章 生活中的轴对称 单元检测卷 题型:解答题
(本题6分) 如图,在11×11的正方形网格中,网格中有一个格点△ABC(即三角形的顶点都在格点上).
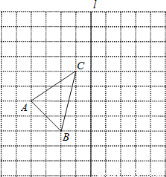
(1)在图中作出△ABC关于直线l对称的△A1B1C1 (要求A与A1,B与B1,C与C1相对应) ;
(2)在直线l上找一点P,使得△PAC的周长最小.
【解析】 试题分析:(1)根据网格结构找出点A、B、C 关于直线l的对称点A1、B1、C1的位置,然后顺次连接即可; (2)有题意知只要让PA+PC最短即可,也就是根据对称的性质,C′A与l的交点即为P点,因此这时候的. △PAC的周长最小.查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册数学 第五章 生活中的轴对称 单元检测卷 题型:单选题
在平面直角坐标系中,以点A(2,4)为圆心,1为半径作⊙A,以点B(3,5)为圆心,3为半径作⊙B,M、N分别是⊙A,⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为( )
A. 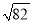 -4 B.
-4 B. 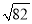 -1 C. 6-2
-1 C. 6-2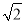 D.
D. 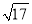 -3
-3
查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册 同步测试 1.2 幂的乘法与积的乘方 题型:单选题
计算(2a)3的结果是( )
A. 6a B. 8a C. 2a3 D. 8a3
D 【解析】试题分析:利用积的乘方以及幂的乘方法则进行计算即可求出答案. 【解析】 (2a)3=8a3; 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com