练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，二次函数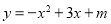的图象与x轴的一个交点为B（4，0），另一个交点为A，且与y轴相交于C点．

    （1）求m的值及C点坐标；

    （2）在直线BC上方的抛物线上是否存在一点M，使得它与B，C两点构成的三角形面积最大，若存在，求出此时M点坐标；若不存在，请简要说明理由；

    （3）P为抛物线上一点，它关于直线BC的对称点为Q．

    ①当四边形PBQC为菱形时，求点P的坐标；

    ②点P的横坐标为t（0＜t＜4），当t为何值时，四边形PBQC的面积最大，请说明理由．

    （1）m=4，C（0，4）；（2）存在，M（2，6）；（3）①P（，）或P（，）；②当t=2时，S四边形PBQC最大=16． 【解析】 试题分析：（1）用待定系数法求出抛物线解析式； （2）先判断出面积最大时，平移直线BC的直线和抛物线只有一个交点，从而求出点M坐标； （3）①先判断出四边形PBQC时菱形时，点P是线段BC的垂直平分线，利用该特殊性建立方程求解； ②先...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年北师大版八年级数学下册 期末测评 题型：解答题

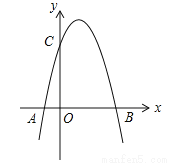
    如图，已知∠BAC=60° ,∠B=80° ,DE垂直平分AC交BC于点D,交AC于点E.

    (1)求∠BAD的度数；

    (2)若AB=10,BC=12,求△ABD的周长.

    （1）20°；（2）22. 【解析】试题分析：（1）根据三角形内角和定理求出∠C，根据线段垂直平分线的性质得到DA=DC，求出∠DAC，计算即可； （2）根据DA=DC，三角形的周长公式计算． 【解析】 (1)∵∠BAC=60°,∠B=80°, ∴∠C=180°-∠BAC-∠B=180°-60°-80°=40°, ∵DE垂直平分AC,∴DA=DC. ∴∠DAC...

    查看答案和解析>>

    科目：初中数学 来源：辽宁省2018届九年级上学期期末考试数学试卷 题型：单选题

    在平面直角坐标系中，点P（2，一 4）关于原点对称的点的坐标是（ ）

    A. （2,4 ） B. （一2，4） C. （一2，一4） D. （一4，2）

    B 【解析】【解析】 点P（2，一 4）关于原点对称的点的坐标是（－2，4）．故选B．

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型：单选题

    一名模型赛车手遥控一辆赛车，先前进1m，然后，原地逆时针方向旋转角a(0°<α<180°)。被称为一次操作．若五次操作后，发现赛车回到出发点，则角α为 ( )

    A. 7 2° B. 108°或14 4° C. 144° D. 7 2°或144°

    D 【解析】试题分析：因为赛车五次操作后回到出发点，五次操作一种是“正五边形“二种是“五角星“形，根据α最大值小于180°，经过五次操作，绝对不可能三圈或三圈以上．一圈360°或两圈720度．分别用360°和720°除以5，就可以得到答案． 【解析】 360÷5=72°， 720÷5=144°． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东海实验学校2017年中考数学模拟试卷 题型：单选题

    下图中①表示的是组合在一起的模块，在②③④⑤四个图形中，是这个模块的俯视图的是（　　）

    A. ② B. ③ C. ④ D. ⑤

    A 【解析】②是该几何体的俯视图；③是该几何体的左视图和主视图；④、⑤不是该几何体的三视图. 故选A.

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省徐州市中考数学一模试卷 题型：解答题

    如图，在△ABC中，D、E分别是AB、AC的中点，过点E作EF∥AB，交BC于点F．

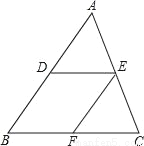
    （1）求证：四边形DBFE是平行四边形；

    （2）当△ABC满足什么条件时，四边形DBFE是菱形？为什么？

    (1)见解析;(2) AB=BC 【解析】试题分析：（1）根据三角形的中位线平行于第三边并且等于第三边的一半可得DE∥BC，然后根据两组对边分别平行的四边形是平行四边形证明. （2）根据邻边相等的平行四边形是菱形证明． 试题解析： （1）∵D、E分别是AB、AC的中点， ∴DE是△ABC的中位线. ∴DE∥BC. 又∵EF∥AB， ∴四边形DBFE是...

    查看答案和解析>>

    科目：初中数学 来源：2017年江苏省徐州市中考数学一模试卷 题型：填空题

    如图，PA、PB是⊙O的切线，切点分别为A、B，已知⊙O的半径为2，∠P=60°，则弦AB的长为_____．

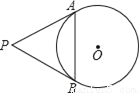
    【解析】连接AO，并延长交⊙O于C，连接BC， ∵PA、PB是⊙O的切线， ∴PA=PB， 又∵∠P=60°， ∴∠PAB=60°； 又∵AC是圆的直径， ∴CA⊥PA，∠ABC=90°， ∴∠CAB=30°， 而AC=4， ∴在Rt△ABC中，cos∠CAB=cos30°=，即， ∴AB=4×． 故答案为： ．

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省中考数学二模试卷 题型：解答题

    （本小题满分13分）

    某公司经销农产品业务，以3万元/吨的价格向农户收购农产品后，以甲、乙两种方式进行销售，甲方式包装后直接销售；乙方式深加工后再销售．甲方式农产品的包装成本为1万元/吨，根据市场调查，它每吨平均销售价格y（单位：万元）与销售量m（单位：吨）之间的函数关系为y = -m+14（2≤m≤8）；乙方式农产品深加工等（不含进价）总费用S（单位：万元）与销售量n（单位：吨）之间的函数关系是S=3n+12，平均销售价格为9万元/吨．

    参考公式：抛物线y＝ax2+bx+c（a≠0）的顶点坐标是（－，）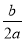

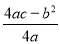    （1）该公司收购了20吨农产品，其中甲方式销售农产品x吨，其余农产品用乙方式销售，经销这20吨农产品所获得的毛利润为w万元（毛利润=销售总收入－经营总成本）．

    ①直接写出：甲方式购买和包装x吨农产品所需资金为_________万元；乙方式购买和加工其余农产品所需资金为_________万元；

    ②求出w关于x的函数关系式；

    ③若农产品全部销售该公司共获得了48万元毛利润，求x的值；

    ④若农产品全部售出，该公司的最小利润是多少．

    （2）该公司现有流动资金132万元，若将现有流动资金全部用于经销农产品，

    ①其中甲方式经销农产品x吨，则总经销量p为__________吨（用含x的代数式表示）；

    ②当x为何值时，使公司获得最大毛利润，并求出最大毛利润．

    （1）①4x，132-6x；②、w=；③、x=7；④、x=8，最小值为40；（2）①；②、以方式A销售4吨时,公司能获得最大毛利润64万元 【解析】 试题分析：（1）根据题意得出函数解析式；②、利用毛利润=销售总收入－经营总成本得出函数关系式；③、将w=48代入解析式求出x的值；④、根据函数的性质求出最值，（2）根据题意得出解析式；②、将m的值代入函数关系式，求出最值． 试题解析...

    查看答案和解析>>

    科目：初中数学 来源：四川省遂宁市2017-2018学年八年级上学期教学水平监测数学试卷 题型：单选题

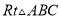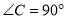    如图在中， ，AD平分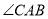，AC=6，BC=8，则CD的长为

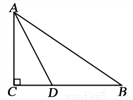
    A. 1 B. 2 C. 3 D. 4

    C 【解析】试题解析：过点D作DE⊥AB于E， ∵AD平分∠BAC， ∴CD=DE， 在Rt△ACD和Rt△AED中， ， ∴Rt△ACD≌Rt△AED（HL）， ∴AE=AC=6， 由勾股定理得，AB==10， ∴BE=AB-AE=10-6=4， 设CD=DE=x，则BD=8-x， 在Rt△BDE中，DE2+BE2=BD2， ...

    查看答案和解析>>

    同步练习册答案