练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    点P（x，y），且xy＜0，则点P在（ ）

    A. 第一象限或第二象限 B. 第一象限或第三象限

    C. 第一象限或第四象限 D. 第二象限或第四象限

    D 【解析】∴x，y异号， 当x>0时，y<0，即点的横坐标大于0，纵坐标小于0，点在第四象限； 当x<0时，y>0，则点的横坐标小于0，纵坐标大于0，点在第二象限。 故选：D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年广东省汕头市潮南区九年级（上）期末数学试卷（a卷） 题型：单选题

    如图，在⊙O中，弦AB∥CD，若∠ABC=40°，则∠BOD=（ ）

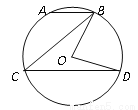
    A. 20° B. 40° C. 50° D. 80°

    D 【解析】试题解析：∵弦AB∥CD， ∴∠ABC=∠BCD， ∴∠BOD=2∠ABC=2×40°=80°． 故选D．

    查看答案和解析>>

    科目：初中数学 来源：江苏省姜堰区2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    将一副三角板如图放置，若∠AOD=30°，则∠BOC=______．

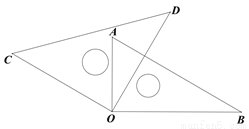
    150° 【解析】利用“两个角的和为90°，则这两个角互余”进行计算即可求解. 【解析】 ∵∠COD=90°，且∠AOD=30°， ∴∠AOC=90°－30°=60°， ∵∠AOB=90°， ∴∠BOC=90°+60°=150°. 故答案为：150°.

    查看答案和解析>>

    科目：初中数学 来源：2018人教版七年级数学下册练习：第七章达标检测卷 题型：解答题

    在平面直角坐标系中描出下列各点A（5，1），B（5，0），C（2，1），D（2，3），并顺次连接，且将所得图形向下平移4个单位，写出对应点A＇、B＇、C＇、D＇的坐标。

    A＇（5，－3）B＇（5，－4）C＇（2，－3）D＇（2，－1） 【解析】试题分析：直接利用平移中点的变化规律求解即可． 试题解析：在平面直角坐标系中各点的位置如图所示： 由点的平移规律可知，点（x，y）向下平移4个单位后的点的坐标是（x，y-4）， ∴平移后各点的坐标分别为A′（5，-3），B′（5，-4），C′（2，-3），D′（2，-1）.

    查看答案和解析>>

    科目：初中数学 来源：2018人教版七年级数学下册练习：第七章达标检测卷 题型：填空题

    已知点A在x轴上方，到x轴的距离是3，到y轴的距离是4，那么点A的坐标是______________。

    (－4，3)或（4，3） 【解析】试题解析：∵点A在轴上方，到轴的距离是3， ∴点A的纵坐标是3， ∵点A到轴的距离是4， ∴点A的横坐标是4或-4． ∴点A的坐标是（4，3）或（-4，3）． 故答案为：（4，3）或（-4，3）．

    查看答案和解析>>

    科目：初中数学 来源：2018届中考数学一轮复习单元检测：第2讲 整式与因式分解 题型：单选题

    用棋子摆出下列一组图形(如图)：

    按照这种规律摆下去，第n个图形用的棋子个数为(　　)

    A. 3n B. 6n

    C. 3n＋6 D. 3n＋3

    D 【解析】观察可知：①中有棋子6个，6=3×1+3， ②中有棋子9个，9=3×2+3， ③中有棋子12个，12=3×3+3， … 所以第n个图形用的棋子个数为：3n+3， 故答案为：3n+3.

    查看答案和解析>>

    科目：初中数学 来源：2018届中考数学一轮复习单元检测：第2讲 整式与因式分解 题型：单选题

    根据如图的程序，计算当输入值x=﹣2时，输出结果y为（　　）

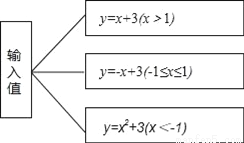
    A. 1 B. 5 C. 7 D. 以上都有可能

    C 【解析】先由x=﹣2≤﹣1，确定x与y的关系式为y=x2+3，然后代值计算即可． 【解析】 ∵x=﹣2≤﹣1， ∴y=x2+3=（﹣2）2+3=7， 故选C．

    查看答案和解析>>

    科目：初中数学 来源：广西合浦县2017年秋季学期教学质量监测八年级数学试卷 题型：单选题

    在一个不透明的口袋中装有4个红球和若干个白球,它们除颜色外其他相同.通过多次摸球试验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有(　　)

    A. 16个 B. 15个 C. 13个 D. 12个

    D 【解析】试题分析：由摸到红球的频率稳定在25%附近得出口袋中得到红色球的概率，进而求出白球个数即可． 【解析】 设白球个数为：x个， ∵摸到红色球的频率稳定在25%左右， ∴口袋中得到红色球的概率为25%， ∴=， 解得：x=12， 故白球的个数为12个． 故选：D．

    查看答案和解析>>

    科目：初中数学 来源：广西合浦县2017年秋季学期教学质量监测九年级数学试卷 题型：填空题

    如图，矩形ABCD中，AD=3，∠CAB=30°，点P是线段AC上的动点，点Q是线段CD上的动点，则AQ+QP的最小值是_____．

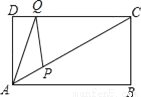
    3 【解析】作点A关于直线CD的对称点E，作EP⊥AC于P，交CD于点Q． ∵四边形ABCD是矩形， ∴∠ADC=90°， ∴DQ⊥AE，∵DE=AD， ∴QE=QA， ∴QA+QP=QE+QP=EP， ∴此时QA+QP最短（垂线段最短）， ∵∠CAB=30°， ∴∠DAC=60°， 在RT△APE中，∵∠APE=90°，AE=2AD=6...

    查看答案和解析>>

    同步练习册答案