
一个圆锥的高为3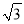 cm,侧面展开图是半圆,
cm,侧面展开图是半圆,
求:(1)圆锥母线与底面半径的比;
(2)锥角的大小;
(3)圆锥的全面积.
(1)2;(2)60°;(3)27π. 【解析】试题分析:(1)根据展开图是半圆,可求得母线与半径比值. (2)利用结论(1)可知锥角大小. (3)由(2)结论,利用特殊三角形计算出底面半径和母线长,分别求出侧面积和底面积. 试题解析: 如图,AO为圆锥的高,经过AO的截面是等腰△ABC,则AB为圆锥母线l,BO为底面半径r. (1)因圆锥的侧面展开图是半圆,所... 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源:《概率的进一步认识》单元测试2 题型:填空题
从装有5个红球和3个白球的袋中任意取4个,那么取到的“至少有1个是红球”与“没有红球”的概率分别为 和 。
1,0 【解析】 试题分析:根据必然事件和不可能事件的概率即可作出判断. 由题意得取到的“至少有1个是红球” 的概率为1,取到的“没有红球”的概率为0.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.3课题学习图案设计 测试 题型:填空题
基本图案在轴对称、平移、旋转变化的过程中,图形的______和______都保持不变.
形状, 大小. 【解析】轴对称、平移、旋转变化都是全等变化,所以在变化的过程中,图形的形状和大小不变,只是位置在变化. 故答案为(1)形状;(2)大小.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 23.1图形的旋转(2)测试 题型:单选题
如图,摆放有五杂梅花,下列说法错误的是(以中心梅花为初始位置)( )
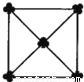
A. 左上角的梅花只需沿对角线平移即可
B. 右上角的梅花需先沿对角线平移后,再顺时针旋转45°
C. 右下角的梅花需先沿对角线平移后,再顺时针旋转180
D. 左下角的梅花需先沿对角线平移后,再顺时针旋转90°
B 【解析】由平移和旋转可得,D选项中左下角的梅花需要先沿着对角线平移后,再逆时针旋转90°,所以B选项错误,故选B.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 24.4弧长和扇形面积(2)练习 题型:填空题
如图,是小芳学习时使用的圆锥形台灯灯罩的示意图,则围成这个灯罩的铁皮的面积为____________ cm2(不考虑接缝等因素,计算结果用π表示).
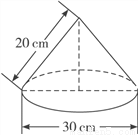
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 24.4弧长和扇形面积(2)练习 题型:填空题
如图,已知圆锥的底面直径为4,母线长为6,则它的全面积为__________.
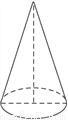
查看答案和解析>>
科目:初中数学 来源:《概率的进一步认识》单元测试4 题型:解答题
一个不透明的口袋里装有红、黄、绿三种颜色的球(除颜色不同外其余都相同),其中红球有2个,黄球有1个,从中任意捧出1球是红球的概率为
(1)试求袋中绿球的个数;

(2)第1次从袋中任意摸出l球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率.
(1)(2) 【解析】试题分析:(1)此题的求解方法是:借助于方程求解;(2)根据简单事件的概率求法解答即可;(3)此题需要两步完成,所以采用树状图或者列表法都比较简单. 试题解析::(1)设绿球的个数为x.由题意,得:,解得x=1,经检验x=1是所列方程的根,所以绿球有1个;(2)P(任意摸出一个球是黄球)=,(3)根据题意,画树状图: 由图知共有12种等可能的结果,即(红1,...查看答案和解析>>
科目:初中数学 来源:《概率的进一步认识》单元测试4 题型:单选题
某市民政部门:“五一”期间举行“即开式福利彩票”的销售活动,发行彩票10万张(每张彩票2元),在这此彩票中,设置如下奖项:
奖金(元) | 1000 | 500 | 100 | 50 | 10 | 2 |
数量(个) | 10 | 40 | 150 | 400 | 1000 | 10000 |
如果花2元钱购买1张彩票,那么所得奖金不少于50元的概率是( )
A. 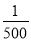 B.
B. 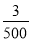 C.
C. 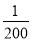 D.
D. 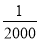
查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 八年级数学上册 全等三角形判定 填空题练习(含答案) 题型:填空题
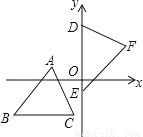
如图,坐标平面上,△ABC≌△FDE,若A点的坐标为(a,1),BC∥x轴,B点的坐标为(b,﹣3),D、E两点在y轴上,则F点到y轴的距离为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com