
��ͼ���ڡ�ABC�͡�DEF�У���B=��DEF��AB=DE����������һ����������Ȼ����֤����ABC�ա�DEF����������ǣ��� ����
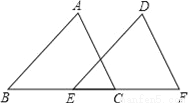
A. ��A=��D B. BC=EF C. ��ACB=��F D. AC=DF
D ���������������� �ߡ�B=��DEF��AB=DE�������ӡ�A=��D������ASA�ɵá�ABC�ա�DEF�� ������BC=EF������SAS�ɵá�ABC�ա�DEF�� �����ӡ�ACB=��F������AAS�ɵá�ABC�ա�DEF�� ��ѡD��
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ�²�4.1.2��ʶ������ ͬ����ϰ ���ͣ���ѡ��
��֪���������ߵij��ֱ���4��10����������ε����ߵij������ǣ����� ��
A. 5 B. 6 C. 11 D. 16
C ���������������Ϊx�������������ߵ����ʣ�6�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��3.2 �ù�ϵʽ��ʾ�ı������ϵ ͬ����ϰ ���ͣ������
��һ�ִ�ϸ���ȵĵ���,Ϊ��ȷ���䳤��,��һ���ϼ���1 m,�Ƶ�����������0.06 kg.
(1)д�����ֵ��߳���������֮��Ĺ�ϵʽ;
(2)���һ��������1 m�������Ϊb kg,��д���������ߵ��ܳ���.
����(1)l= (2) m ����������������� ��1�����������ߵ�����Ϊkg���������֪�����ֵ���1������Ϊ0.06kg���ɴ˿ɵ��������ߵij����ף� ��2���ɣ�1���ɵã�����1��ĵ��ߵij���Ϊ�� �ף��ɴ˿ɵ��������ߵ��ܳ���Ϊ�� ��. ��������� ��1������ߵij���Ϊ�ף�����Ϊm kg�����������ߵij���Ϊ�� �� ��2���ɣ�1����֪��ʣ�µ�kg�ĵ��ߵij���Ϊ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��4.3.3 �á��߽DZߡ��ж�������ȫ�� ͬ����ϰ ���ͣ������
��ͼ,��O���߶�AB���߶�CD���е�.��˵��:
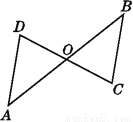
(1)��AOD�ա�BOC;
(2)AD��BC.
(1)�𰸼�����;(2)�𰸼����� �������������������1�����е㶨�壬�õ�AO=BO��CO=DO���Ӷ�ͨ��SAS֤����AOD�ա�BOC�� ��2���ɣ�1���н��ۣ����Եõ���A=��B�������ڴ�����ȣ���ֱ��ƽ�м��ɵó����ۣ� ����������������� (1)�ߵ�O���߶�AB���߶�CD���е㣬��AO=BO��CO=DO�� �ڡ�AOD�͡�BOC�У���AO=BO����AOD=��BOC��DO...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��4.3.3 �á��߽DZߡ��ж�������ȫ�� ͬ����ϰ ���ͣ���ѡ��
��ͼ,AA',BB'��ʾ����������ͬ��ľ��,��O��AA',BB'���е�,������AB=9 cm,���������ھ�A'B'Ϊ(����)
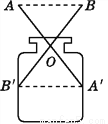
A. 8 cm B. 9 cm C. 10 cm D. 11 cm
B ���������������� ������֪��OA=OA�䣬��AOB=��A��OB�䣬OB=OB�䣬���AOB�ա�A��OB�䣬��A��B��=AB=9cm����ѡB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ��3.3 ��ͼ���ʾ�ı������ϵ ͬ����ϰ ���ͣ���ѡ��
�������糿��������Ӽ������ȥ��ɽ��������������������������60min��ؼң�ͼ�е����߶�OA��AB��BC��������������λ����ҵľ���s��km��������ʱ��t��min��֮��ĺ�����ϵ��������ͼ���п��Դ������������������ߵ�·���ǣ� ��
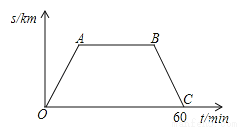
A��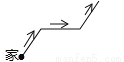 B��
B��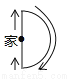 C��
C��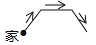 D��
D��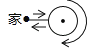
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�²������4.4�ó߹��������ο�ʱ��ϰ ���ͣ������
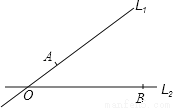
��ͼ���зֱ��A��B��������վ�Ĺ�·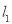 ��
��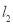 �ཻ�ڵ�O�������ڡ�AOB�ڽ�һ���Ϳ⣬Ҫ���Ϳ��λ�õ�P���㵽A��B��������վ�ľ�����ȣ�����P��������·
�ཻ�ڵ�O�������ڡ�AOB�ڽ�һ���Ϳ⣬Ҫ���Ϳ��λ�õ�P���㵽A��B��������վ�ľ�����ȣ�����P��������·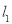 ��
��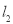 �ľ���Ҳ��ȣ����ó߹���ͼ������P����д������������ͼ�ۼ���
�ľ���Ҳ��ȣ����ó߹���ͼ������P����д������������ͼ�ۼ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�²������4.4�ó߹��������ο�ʱ��ϰ ���ͣ���ѡ��
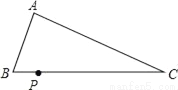
��ͼ����֪��ABC��AC��BC�����ó߹���BC��ȷ��һ��P��ʹPA+PC=BC�������Ҫ�����ͼ�ۼ��ǣ�������
A. 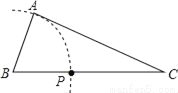 B.
B. 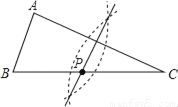 C.
C. 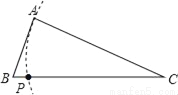 D.
D. 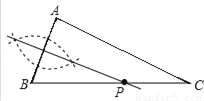
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�걱ʦ�����꼶��1.5��ƽ���ʽ����ϰ�� ���ͣ������
��֪��x2+xy+y=14��y2+xy+x=28����x+y��ֵ��
-7��6 �������������������x2+xy+y=14��y2+xy+x=28���������x2+2xy+y2+x+y=42������εã�x+y��2+��x+y��-42=0����x+y�������壬������ʽ�ֽⷨ�������x+y��ֵ�� ��������� ��x2+xy+y=14�٣�y2+xy+x=28�ڣ� ���+�ڣ��ã�x2+2xy+y2+x+y=42�� �ࣨx+y��2+��x+y��-42=0�� ...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com