
下列四个角中,最有可能与70°角互补的角是( )
A. 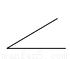 B.
B. 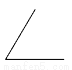 C.
C.  D.
D. 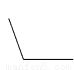
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题七年级北师大版数学试卷(A卷) 题型:单选题
如图是一个正方体的表面展开图,若正方体中相对的面上的数或式子互为相反数,则2x+y的值为( )

A. 0 B. -1 C. -2 D. 1
B 【解析】【解析】 正方体的表面展开图,相对的面之间一定相隔一个正方形.“5”与“2x﹣3”是相对面,“y”与“x”是相对面,“﹣2”与“2”是相对面,∵相对的面上的数字或代数式互为相反数,∴2x﹣3+5=0,x+y=0,解得x=﹣1,y=1,∴2x+y=2×(﹣1)+1=﹣2+1=﹣1.故选B.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 大题易丢分 题型:解答题
阅读理解题:
定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:(5+i)×(3﹣4i)=19﹣17i.
(1)填空:i3= ,i4= .
(2)计算:(4+i)2.
(3)试一试:请利用以前学习的有关知识将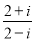 化简成a+bi的形式.
化简成a+bi的形式.
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-17学年度第一学期期末教学质量检测七年级数学试卷 题型:解答题
解方程: 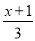 ?1=
?1=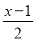
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-17学年度第一学期期末教学质量检测七年级数学试卷 题型:单选题
已知线段AB和点P,如果PA+PB=AB,那么下列结论一定正确的是( )
A. 点P在线段AB上 B. 点P为线段AB的中点
C. 点P在线段AB外 D. 点P在线段AB的延长线上
A 【解析】如图: 因为PA+PB=AB, 所以点P在线段AB上. 故选:A.查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
已知,抛物线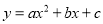 ( a≠0)经过原点,顶点为A(h,k)(h≠0).
( a≠0)经过原点,顶点为A(h,k)(h≠0).
(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线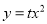 (t≠0)也经过A点,求a与t之间的关系式;
(t≠0)也经过A点,求a与t之间的关系式;
(3)当点A在抛物线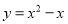 上,且-2≤h<1时,求a的取值范围.
上,且-2≤h<1时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:填空题
如图, 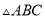 内接于⊙
内接于⊙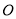 ,
, 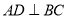 于点
于点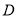 ,
, 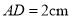 ,
, 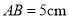 ,
, 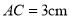 ,则⊙
,则⊙ 的直径是__________.
的直径是__________.

查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:解答题
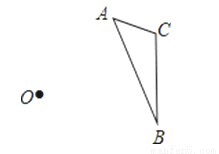
如图,以O为位似中心,将△ABC放大为原来的2倍.
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(二) 题型:单选题
如图,AB为⊙O的切线,切点为B,连接AO,AO与⊙O交于点C,BD为⊙O的直径,连接CD.若∠A=30°,⊙O的半径为2,则图中阴影部分的面积为( )
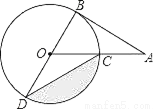
A. 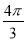 ﹣
﹣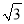 B.
B. 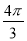 ﹣2
﹣2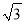 C. π﹣
C. π﹣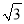 D.
D. 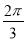 ﹣
﹣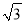
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com