
如图, 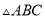 内接于⊙
内接于⊙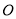 ,
, 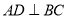 于点
于点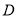 ,
, 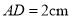 ,
, 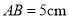 ,
, 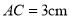 ,则⊙
,则⊙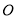 的直径是__________.
的直径是__________.

科目:初中数学 来源:黄金30题系列 八年级数学 小题好拿分 题型:填空题
若(x+k)(x-4)的展开式中不含有x的一次项,则k的值为_________.
4 【解析】试题分析:原式=+(k-4)x-4k,根据题意得:k-4=0,解得:k=4.查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-17学年度第一学期期末教学质量检测七年级数学试卷 题型:解答题
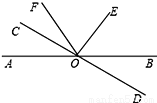
如图,已知直线AB和CD相交于点O,∠COE=90°,OF平分∠AOE.
(1)写出∠AOC与∠BOD的大小关系并说明理由;
(2)若∠COF=34°26′,求∠BOD.
查看答案和解析>>
科目:初中数学 来源:安徽省合肥市2016-17学年度第一学期期末教学质量检测七年级数学试卷 题型:单选题
下列四个角中,最有可能与70°角互补的角是( )
A. 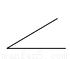 B.
B. 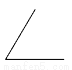 C.
C.  D.
D. 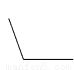
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
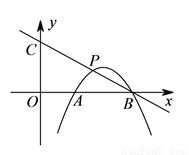
如图,在平面直角坐标系中,抛物线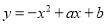 交
交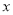 轴于点
轴于点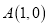 ,
, 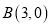 两点,点
两点,点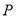 是抛物线上在第一象限内的一点,直线
是抛物线上在第一象限内的一点,直线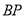 与
与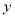 轴相交于点
轴相交于点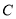 .
.
( )当点
)当点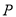 是线段
是线段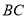 的中点时,求点
的中点时,求点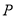 的坐标.
的坐标.
(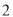 )在(
)在(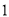 )的条件,求
)的条件,求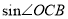 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
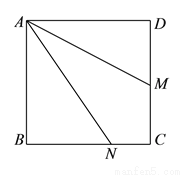
如图,正方形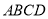 中,
中, 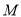 为
为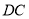 的中点,
的中点, 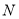 为
为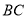 上一点,
上一点, 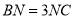 ,设
,设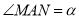 ,则
,则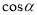 的值等于( ).
的值等于( ).
A. 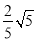 B.
B. 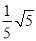 C.
C. 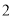 D.
D. 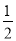
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2018届九年级上学期期中考试数学试卷(含解析) 题型:单选题
二次函数有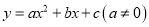 的图象如图,则函数值
的图象如图,则函数值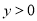 时,
时, 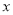 的取值范围是( ).
的取值范围是( ).

A. 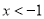 B.
B. 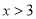 C.
C. 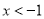 或
或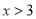 D.
D. 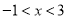
查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:单选题
如图所示的抛物线对称轴是直线x=1,与x轴有两个交点,与y轴交点坐标是(0,3),把它向下平移2个单位后,得到新的抛物线解析式是 y=ax2+bx+c,以下四个结论:
①b2﹣4ac<0,②abc<0,③4a+2b+c=1,④a﹣b+c>0中,判断正确的有( )
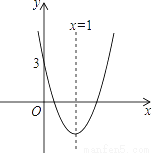
A. ②③④ B. ①②③ C. ②③ D. ①④
A 【解析】 根据题意平移后的抛物线的对称轴x=-=1,c=3-2=1, 由图象可知,平移后的抛物线与x轴有两个交点, ∴b2﹣4ac>0,故①错误; ∵抛物线开口向上, ∴a>0, ∴b<0, ∴abc<0,故②正确; ∵平移后抛物线与y轴的交点为(0,1),对称轴x=1, ∴点(2,1)是点(0,1)的对称点, ∴当x=2时,y...查看答案和解析>>
科目:初中数学 来源:山东省临朐县沂山风景区2017-2018学年八年级上期末模拟数学试卷 题型:解答题
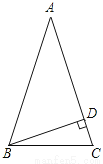
如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com