练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    先化简，再求值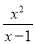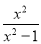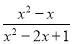：（﹣）÷，其中x是方程3x2﹣x﹣1=0的根．

    ， . 【解析】试题分析：先根据分式混合运算的法则把原式进行化简，再求出x的值，把x的值代入化简后的式子进行计算即可． 试题解析：原式=×=×=， ∵3x2﹣x﹣1=0， ∴x+1=3x2， ∴原式==．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017年甘肃省张掖市中考数学三模试卷 题型：填空题

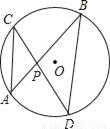
    如图，在⊙O中，弦AB，CD相交于点P．若∠A=40°，∠APD=75°，则∠B=　 　．

    35°． 【解析】试题解析： 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省随州市中考数学模拟试卷 题型：解答题

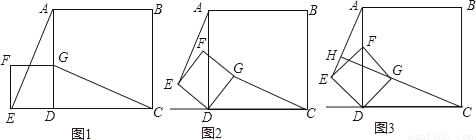
    （1）如图1，正方形ABCD和正方形DEFG，G在AD边上，E在CD的延长线上．求证：AE=CG，AE⊥CG；

    （2）如图2，若将图1中的正方形DEFG绕点D顺时针旋转角度θ（0°＜θ＜90°），此时AE=CG还成立吗？若成立，请给予证明；若不成立，请说明理由；

    （3）如图3，当正方形DEFG绕点D顺时针旋转45°时，延长CG交AE于点H，当AD=4，DG=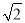时，求线段CH的长．

    （1）（2）见解析；（3）． 【解析】试题分析：（1）先判断出△ADE≌△CDG，然后用互余判断出垂直； （2）先判断出△ADE≌△CDG，然后用互余判断出垂直； （3）先判断出△ADE≌△CDG，然后用互余判断出垂直，然后用勾股定理计算出CM，AM最后用相似即可． 试题解析：（1）在△ADE和△CDG中， DE=DG，∠ADE=∠CDG，AD=CD， ∴△AD...

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省随州市中考数学模拟试卷 题型：单选题

    等腰三角形的一个角是80°，则它的底角是（ ）

    A. 50° B. 80° C. 50°或80° D. 20°或80°

    C 【解析】当80°为顶角时，此时底角度数为=50°； 当80°为底角时，此时顶角度数为180-2×80°=20°. 故它的底角是50°或80°. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：2017年黑龙江省大庆市中考数学三模试卷 题型：解答题

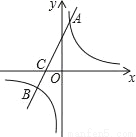
    如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数y=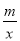（m≠0）的图象交于A、B两点，与x轴交于C点，点A的坐标为（n，6），点C的坐标为（﹣2，0），且tan∠ACO=2．

    （1）求该反比例函数和一次函数的解析式；

    （2）求点B的坐标．

    （1）反比例函数的解析式为，一次函数的解析式为y=2x+4；（2）点B坐标为（﹣3，﹣2）. 【解析】试题分析：（1）先过点A作AD⊥x轴，根据tan∠ACO=2，求得点A的坐标，进而根据待定系数法计算两个函数解析式；（2）先联立两个函数解析式，再通过解方程求得交点B的坐标即可． 试题解析：（1）过点A作AD⊥x轴，垂足为D．由A（n，6），C（﹣2，0）可得，OD=n，AD=6，CO...

    查看答案和解析>>

    科目：初中数学 来源：2017年黑龙江省大庆市中考数学三模试卷 题型：填空题

    已知关于x的分式方程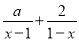=1的解是非负数，则a的取值范围是_____．

    a≥1且a≠2 【解析】分式方程去分母得：a﹣2=x﹣1， 解得：x=a﹣1， 由方程的解为非负数，得到a﹣1≥0，且a﹣1≠1， 解得：a≥1且a≠2． 故答案为：a≥1且a≠2．

    查看答案和解析>>

    科目：初中数学 来源：2017年黑龙江省大庆市中考数学三模试卷 题型：单选题

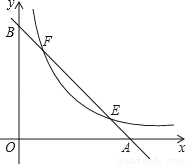
    如图，已知直线y=﹣x+2分别与x轴，y轴交于A，B两点，与双曲线y=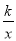交于E，F两点，若AB=2EF，则k的值是（　　）

    A. ﹣1 B. 1 C. 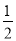D.

    D 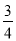【解析】作FH⊥x轴，EC⊥y轴，FH与EC交于D，如图， A点坐标为（2，0），B点坐标为（0，2），OA=OB， ∴△AOB为等腰直角三角形， ∴AB=OA=2， ∴EF=AB=， ∴△DEF为等腰直角三角形， ∴FD=DE=EF=1， 设F点横坐标为t，代入y=﹣x+2，则纵坐标是﹣t+2，则F的坐标是：（t，﹣t+2），E点坐标为（t+1...

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省黄冈市中考数学二模试卷 题型：填空题

    如图，直线y=kx+b经过A（3，1）和B（6，0）两点，则不等式组0＜kx+b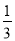＜ x的解集为　 　．

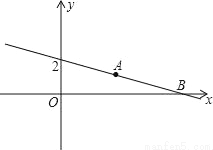
    3＜x＜6． 【解析】将A（3，1）和B（6，0）分别代入y=kx+b得，解得，则函数解析式为y=﹣x+2．可得不等式组，解得3＜x＜6． 故答案为:3＜x＜6．

    查看答案和解析>>

    科目：初中数学 来源：吉林省长春市区2018届九年级上期末模拟数学试卷（解析版） 题型：解答题

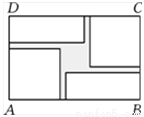
    如图,某旅游景点要在长、宽分别为20米、12米的矩形水池的正中央建一个与矩形的边互相平行的正方形观赏亭,观赏亭的四角连接四条与矩形的边互相平行且宽度相等的道路,已知道路的宽为正方形边长的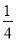,若道路与观赏亭的面积之和是矩形水池面积的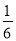,求道路的宽．

    道路的宽为1米 【解析】试题分析：首先假设道路的宽为x米，根据道路的宽为正方形边长的，得出正方形的边长以及道路与正方形的面积进而得出答案． 试题解析：设道路的宽为x米，则可列方程： x（12﹣4x）+x（20﹣4x）+16x2=×20×12， 即：x2+4x﹣5=0， 解得：x1=l，x2=﹣5（舍去）． 答：道路的宽为1米．

    查看答案和解析>>

    同步练习册答案