
以正方形ABCD的BC边为直径作半圆O,过点D作直线切半圆于点F,交AB边于点E.则三角形ADE和直角梯形EBCD周长之比为( )
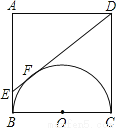
A. 4:5 B. 5:6 C. 6:7 D. 7:8
C科目:初中数学 来源:北京市2017-2018学年第一学期初二数学期中试卷 题型:解答题
已知:如图,Rt△ABC中,∠BAC=90°

(1)按要求作图:(保留作图痕迹)
①延长BC到点D,使CD=BC;
②延长CA到点E,使AE=2CA;
③连接AD,BE并猜想线段 AD与BE的大小关系;
(2)证明(1)中你对线段AD与BE大小关系的猜想.
见解析 【解析】试题分析:(1)根据基本作图,作一条线段等于已知线段的作图方法就可以作出图形; (2)延长AC到点F,使CF=AF,连接BF,证明△ACD≌△FCB,就有AD=FB,进而得出AE=AF,就可以得出BE=BF,从而结论AD=BE. 试题解析:(1)由题意,得作图如下: (2)延长AC到点F,使CF=AF,连接BF, 在△ACD和△FCB中, CD=...查看答案和解析>>
科目:初中数学 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:填空题
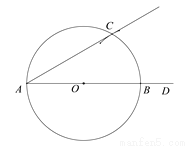
下面是“作一个角等于30°”的尺规作图过程.
作法:如图,(1)作射线AD;
(2)在射线AD上任意取一点O(点O不与点A重合);
(3)以点O为圆心,OA为半径作⊙O,交射线AD于点B;
(4)以点B为圆心,OB为半径作弧,交⊙O于点C;
(5)作射线AC.
∠DAC即为所求作的30°角.
请回答:该尺规作图的依据是_________________.
查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:解答题
某农户生产经销一种农副产品,已知这种产品的成本价为20元/千克.市场调查发现,该产品每天的销售量w (千克)与销售价x (元/千克)有如下关系:w=﹣2x+80.设这种产品每天的销售利润为y (元).
(1)求y与x之间的函数关系式,自变量x的取值范围;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?(参考关系:销售额=售价×销量,利润=销售额﹣成本)
(1) y=﹣2x2+120x﹣1600,20≤x≤40;(2) 30元/千克, 200元;(3)25. 【解析】 试题分析:(1)根据销售利润y=(每千克销售价﹣每千克成本价)×销售量w,即可列出y与x之间的函数关系式; (2)先利用配方法将(1)的函数关系式变形,再利用二次函数的性质即可求解; (3)先把y=150代入(1)的函数关系式中,解一元二次方程求出x,再根据x...查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:解答题
如图,图形中每一小格正方形的边长为1,已知△ABC
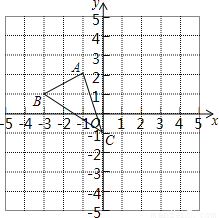
(1)AC的长等于 .(结果保留根号)
(2)将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 ;
(3)画出将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C1,并写出A点对应点A1的坐标?
(1)(2)(1,2)(3)图形见解析 【解析】试题分析:(1)根据图形,可得出AC的坐标,可得纵横坐标的关系,进而可求出AC的长; (2)根据图形,可得出ABC的坐标,向右平移2个单位可得A'的坐标; (3)根据旋转的规律,把△OAB的绕点O按顺时针方向旋转90°,就是把它上面的各个点按顺时针方向旋转90°,可得A1的坐标. 试题解析:(1)根据勾股定理可得AC=; (2)...查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:单选题
如图,PA,PB是⊙O的两条切线,切点是A,B.如果OP=4,OA=2,那么∠AOB=( )

A. 90° B. 100° C. 120° D. 150°
C 【解析】由切线长定理知△APO≌△BPO,得∠AOP=∠BOP.可求得cos∠AOP=2:4=,所以可知∠AOP=60°,从而求得∠AOB=120°. 故选:C.查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:解答题
如图,已知,在锐角△ABC中,CE⊥AB于点E,点D在边AC上,联结BD交CE于点F,且EF·FC=FB·DF.
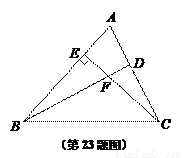
(1)求证:BD⊥AC;
(2)联结AF,求证:AF·BE=BC·EF.
(1)详见解析;(2)详见解析. 【解析】试题分析:(1)由两边成比例且夹角相等的两个三角形相似,可得△EFB∽△DFC,再由相似三角形对应角相等得∠FEB=∠FDC = 90°,即可得证; (2)由△EFB∽△DFC得∠ABD =∠ACE,进而△AEC∽△FEB,由相似三角形对应边成比例得,由此△AEF∽△CEB,可得. 试题解析:(1)∵AF·BE=BC·EF , ∴,...查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:单选题
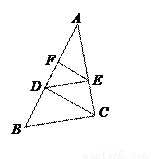
如图,已知点D、F在△ABC的边AB上,点E在边AC上,且DE∥BC,要使得EF∥CD,还需添加一个条件,这个条件可以是
A. 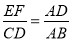 ; B.
; B. 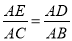 ;
;
C. 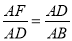 ; D.
; D. 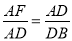 .
.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:单选题
如图,梯形ABCD中,DC∥AB ,EF是梯形的中位线,对角线BD交EF于G,若AB=10,EF=8,则GF的长等于( )
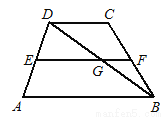
A. 2 B. 3 C. 4 D. 5
B 【解析】∵EF是梯形ABCD的中位线,AB∥CD, ∴EF∥AB, ∴DG=BG, ∴EG=1/2AB=5 ∴GF=EF-EG=8-5=3. 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com