
如图,图形中每一小格正方形的边长为1,已知△ABC
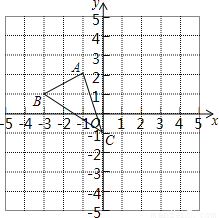
(1)AC的长等于 .(结果保留根号)
(2)将△ABC向右平移2个单位得到△A′B′C′,则A点的对应点A′的坐标是 ;
(3)画出将△ABC绕点C按顺时针方向旋转90°后得到△A1B1C1,并写出A点对应点A1的坐标?
(1)(2)(1,2)(3)图形见解析 【解析】试题分析:(1)根据图形,可得出AC的坐标,可得纵横坐标的关系,进而可求出AC的长; (2)根据图形,可得出ABC的坐标,向右平移2个单位可得A'的坐标; (3)根据旋转的规律,把△OAB的绕点O按顺时针方向旋转90°,就是把它上面的各个点按顺时针方向旋转90°,可得A1的坐标. 试题解析:(1)根据勾股定理可得AC=; (2)...科目:初中数学 来源:四川省江县初中2016年秋季八年级期末考试试卷 题型:单选题
若 是一个完全平方式,则常数
是一个完全平方式,则常数 的值为( )
的值为( )
A. 11 B. 21 C. -19 D. 21或—19
D 【解析】已知是一个完全平方式,可得k-1=±20,,解得k=21或k=-19,故选D.查看答案和解析>>
科目:初中数学 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:解答题
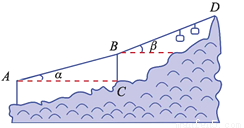
缆车,不仅提高了景点接待游客的能力,而且解决了登山困难者的难题.如图,当缆车经过点A到达点B时,它走过了700米.由B到达山顶D时,它又走过了700米.已知线路AB与水平线的夹角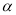 为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
查看答案和解析>>
科目:初中数学 来源:北京市平谷区2018届初三第一学期期末数学试卷 题型:单选题
如图,Rt△ABC中,∠C=90°,∠A=30°,CD⊥AB于D,则△CBD与△ABC的周长比是( )
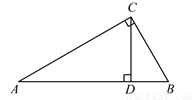
A. 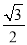 B.
B. 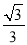 C.
C. 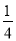 D.
D. 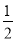
查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:解答题
如图,⊙O的直径AB=6cm,D为⊙O上一点,∠BAD=30°,过点D的切线交AB的延长线于点C.求∠ADC的度数及AC的长.
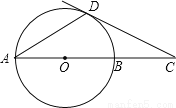
查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:单选题
以正方形ABCD的BC边为直径作半圆O,过点D作直线切半圆于点F,交AB边于点E.则三角形ADE和直角梯形EBCD周长之比为( )
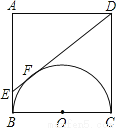
A. 4:5 B. 5:6 C. 6:7 D. 7:8
C查看答案和解析>>
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:单选题
下列命题:(1)经过三点一定可以作圆;(2)任一个三角形一定有一个外接圆,而且只有一个外接圆;(3)任意一个圆一定有一个内接三角形,而且只有一个内接三角形;(4)三角形的外心到三角形三个顶点的距离相等.上述结论中正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】根据在同一平面内,经过不在同一直线上的三点,确定一个圆,可知(1)不正确,(2)正确;任意一个圆有无数个内接三角形,(3)不正确;三角形的外心是三角形三条垂直平分线的交点,所以到三角形三个顶点的距离相等,故(4)正确. 故选:B.查看答案和解析>>
科目:初中数学 来源:上海浦东新区2017-2018学年九年级上学期期末数学试卷(初三一模) 题型:填空题
计算:3tan30°+sin45°= .
【解析】3tan30°+sin45°==. 故答案为:查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:解答题
学校课外生物小组的试验园地是长35米、宽20米的矩形,为便于管理,现要在中间开辟一横两纵三条等宽的小道(如图),要使种植面积为600平方米,求小道的宽.若设小道的宽为x米,则可列方程为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com