
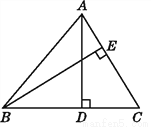
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,若BC=10,AC=8,BE=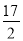 ,求AD的长.
,求AD的长.
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源:北师大版七年级下册4.3.2探索三角形全等的条件练习 题型:单选题
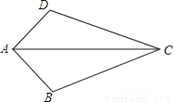
如图,AC平分∠BAD,∠B=∠D,AB=8cm,则AD=( )
A. 6cm B. 8cm C. 10cm D. 4cm
B 【解析】∵AC平分∠BAD, ∴∠DAC=∠BAC, 在△ADC和△ABC中, ∠B=∠D,∠DAC=∠BAC,AC=AC, ∴△ADC≌△ABC(AAS), ∴AD=AB=8cm. 故选:B.查看答案和解析>>
科目:初中数学 来源:北师大七年级下1.7 整式的除法 同步练习含答案 题型:解答题
计算:
(1)(3a2b)3·(-2ab4)2÷6a5b3;
(2)7x3y2÷ .
.
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型:单选题
下列长度的三条线段能组成三角形的是( )
A. 5,6,10 B. 5,6,11 C. 3,4,8 D. 4a,4a,8a(a>0)
A 【解析】 试题解析:根据三角形任意两边的和大于第三边,得 A中,5+6=11>10,能组成三角形; B中,5+6=11,不能组成三角形; C中,3+4=7<8,不能够组成三角形; D中,4a+4a=8a,不能组成三角形. 故选A.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型:单选题
△ABC的三边长a,b,c满足关系式(a-b)(b-c)(c-a)=0,则这个三角形一定是( )
A. 等腰三角形 B. 等边三角形 C. 等腰直角三角形 D. 无法确定
A 【解析】∵(a-b)(b-c)(c-a)=0, ∴a-b=0或b-c=0或c-a=0, ∴a=b或b=c或c=a, 又∵a、b、c是△ABC的三边, ∴△ABC是等腰三角形. 故选A.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型:单选题
如图,△ABC的面积为16,点D是BC边上一点,且BD=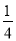 BC,点G是AB边上一点,点H在△ABC内部,BD∥GH,且BD=GH.则图中阴影部分的面积是( )
BC,点G是AB边上一点,点H在△ABC内部,BD∥GH,且BD=GH.则图中阴影部分的面积是( )
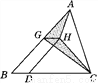
A. 3 B. 4 C. 5 D. 6
B 【解析】试题分析:设△ABC底边BC上的高为h,△AGH底边GH上的高为h1,△CGH底边GH上的高为h2, 则有h=h1+h2.所以S△ABC=BC•h=16,S阴影=S△AGH+S△CGH=GH•h1+GH•h2=GH•(h1+h2)=GH•h.因为四边形BDHG是平行四边形,且BD=BC,可得GH=BD=BC,所以S阴影=×(BC•h)=S△ABC=4. 故答案选B. ...查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型:单选题
下列说法中正确的是( )
A. 三角形的角平分线和中线都是线段
B. 三角形的角平分线和中线都是射线
C. 三角形的角平分线是射线,而中线是线段
D. 三角形的角平分线是线段,而中线是射线
A 【解析】【解析】 三角形的角平分线和中线都是线段.故选A.查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型:单选题
如图,小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是( )
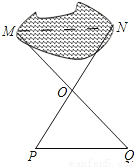
A. PO B. PQ C. MO D. MQ
B 【解析】试题分析: 则只需测出PQ的长即可求出M、N之间的距离.故选B.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
如图,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为________.
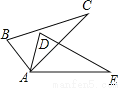
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com