练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    △ABC的三边长a,b,c满足关系式(a-b)(b-c)(c-a)=0,则这个三角形一定是(　　)

    A. 等腰三角形 B. 等边三角形 C. 等腰直角三角形 D. 无法确定

    A 【解析】∵(a-b)(b-c)(c-a)=0， ∴a-b=0或b-c=0或c-a=0， ∴a=b或b=c或c=a， 又∵a、b、c是△ABC的三边， ∴△ABC是等腰三角形. 故选A.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级下册4.3.2探索三角形全等的条件练习 题型：解答题

    如图1，在锐角△ABC中，AD⊥BC于D，BE⊥AC于E，AD与BE相交于F，且BF=AC。求证：ED平分∠FEC。

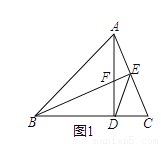
    证明见解析 【解析】分析：求出∠DBF=∠DAC，由AAS证明△BDF≌△ADC．得出对应边相等BD=AD，由等腰直角三角形的性质得出∠BAD=∠ABD=45°，证明A、B、D、E四点共圆，由圆周角定理得出∠BED=∠BAD=45°，得出∠CED=∠BED，即可得出结论. 本题解析： ∵AD⊥BC，BE⊥AC， ∴∠BDF=∠ADC=90°，∠AEB=∠FEC=90°， ...

    查看答案和解析>>

    科目：初中数学 来源：北师大七年级下1.7 整式的除法 同步练习含答案 题型：解答题

    计算:(66x6y3-24x4y2+3x2y)÷(-3x2y).

    -22x4y2+8x2y-1. 【解析】试题分析：用多项式66x6y3-24x4y2+3x2y中的每一项分别除以单项式-3x2y，再把所得的商相加． 解:原式=-22x4y2+8x2y-1.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型：单选题

    一个等腰三角形的两边长分别是3和7，则它的周长为（　　）

    A. 17 B. 15 C. 13 D. 13或17

    A 【解析】试题分析：当3为腰时，则3+3=6＜7，不能构成三角形，则等腰三角形的腰长为7，底为3，则周长为：7+7+3=17.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型：单选题

    若一个三角形的两边长分别为3和7，则第三边长可能是（ ）

    A．6 B．3 C．2 D．11

    A. 【解析】 试题分析：根据三角形三边关系，两边之和第三边，两边之差小于第三边可得4＜第三边长＜10，所以符合条件的整数为6，故答案选A．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型：解答题

    如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,若BC=10,AC=8,BE=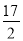,求AD的长.

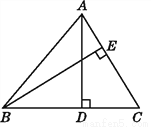
    6.8 【解析】试题分析：根据S△ABC=·BC·AD=·AC·BE即可得出结论． 试题解析：【解析】 因为AD⊥BC，BE⊥AC，所以S△ABC=·BC·AD=·AC·BE．所以BC·AD=AC·BE．又因为BC=10，AC=8，BE=，所以10AD=8×，所以AD=6.8．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型：填空题

    如图,在△ABC中,BC边上的高是____;在△BCE中,BE边上的高是____;在△ACD中,AC边上的高是____.

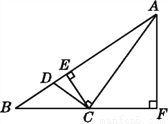
    AF CE CD 【解析】【解析】 在△ABC中，BC边上的高是AF；在△BCE中，BE边上的高是CE；在△ACD中，AC边上的高是CD．故答案为：AF，CE，CD．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型：单选题

    把等腰直角三角形的三角板按如图所示的方式立在桌面上，顶点A顶着桌面，若另两个顶点分别距离桌面5cm和3cm，则过另外两个顶点向桌面作垂线，则垂足之间的距离即DE的长为( )

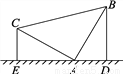
    A. 4cm B. 6cm C. 8cm D. 求不出来

    C 【解析】∵ ∠BAC=90° ∠AEC=90° ∴ ∠BAC=∠AEC ∵ ∠DAB+∠BAC=∠DAC ∠ECA+∠AEC=∠DAC ∠BAC=∠DEC ∴ ∠ECA=∠DAB ∵ △ABD是直角三角形 △CAE是直角三角形 AB=AC ∠ECA=∠DAB ∴ △ABD≌△CAE (一边一锐角对应相等的两个直角三角形全等) ∴ AE=BD AD=CE...

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

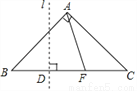
    如图，等腰Rt△ABC中，AB=AC=1，点F是边BC上不与点B、C重合的一个动点，直线l垂直平分BF，垂足为D，当△AFC是等腰三角形时，BD的长为________．

    或 【解析】试题解析：∵等腰Rt△ABC中，AB=AC=1， ∴BC=， 分两种情况： ①当AF=CF时，∠FAC=∠C=45°， ∴∠AFC=90°， ∴AF⊥BC， ∴BF=CF=， ∵直线l垂直平分BF， ∴BD=BF=； ②当CF=CA=1时，BF=BC-CF=， ∵直线l垂直平分BF， ∴BD=BF=； 故答案...

    查看答案和解析>>

    同步练习册答案