练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，丁轩同学在晚上由路灯AC走向路灯BD，当他走到点P时，发现身后他影子的顶部刚好接触到路灯AC的底部，当他向前再步行20m到达Q点时，发现身前他影子的顶部刚好接触到路灯BD的底部，已知丁轩同学的身高是1.5m，两个路灯的高度都是9m，则两路灯之间的距离是（　 　）

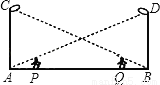
    A. 24m B. 25m C. 28m D. 30m

    D 【解析】由题意可得:EP∥BD,所以△AEP∽△ADB,所以,因为EP=1.5,BD=9,所以,解得:AP=5,因为AP=BQ,PQ=20,所以AB=AP+BQ+PQ=5+5+20=30,故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖北省武汉市江夏区2018届九年级上期末模拟数学试卷 题型：单选题

    用配方法解方程x2-4x+2=0，下列配方正确的是（   ）

    A. （x-2）2=2 B. （x+2）2=2 C. （x-2）2=-2 D. （x-2）2=6

    A 【解析】把方程x2-4x+2=0的常数项移到等号的右边，得到x2-4x=-2， 方程两边同时加上一次项系数一半的平方，得到x2-4x+4=-2+4， 配方得（x-2)2=2， 故选：A．

    查看答案和解析>>

    科目：初中数学 来源：山东省临朐县沂山风景区2018届九年级上期末模拟数学试卷 题型：填空题

    若关于x的方程kx2+2x+1=0有两个实根，则k的取值范围是________．

    k≤1且k≠0 【解析】试题解析：依题意列方程组 解得k＜1且k≠0．

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型：解答题

    如图，在△ABC中，AB=AC，以AC为直径的⊙O交AB于点D，交BC于点E．

    （1）求证：BE=CE；

    （2）若BD=2，BE=3，求AC的长．

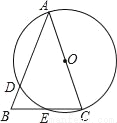
    (1)证明见解析；（2）9. 【解析】试题分析：（1）连结AE，如图，根据圆周角定理，由AC为⊙O的直径得到∠AEC=90°，然后利用等腰三角形的性质即可得到BE=CE； （2）连结DE，如图，证明△BED∽△BAC，然后利用相似比可计算出AB的长，从而得到AC的长． 试题解析：（1）证明：连结AE，如图，∵AC为⊙O的直径，∴∠AEC=90°，∴AE⊥BC，而AB=AC，∴BE...

    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型：填空题

    如图，AB∥CD∥EF，AF与BE相交于点G，且AG＝2，GD＝1，DF＝5，那么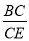的值等于________．

    【解析】【解析】 ∵AB∥CD∥EF，∴ ，故答案为： ．

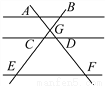
    查看答案和解析>>

    科目：初中数学 来源：浙江省宁波市东钱湖九校2018届九年级上册期中联考数学试卷 题型：单选题

    在△ABC中，若|sinA﹣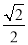|+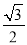（﹣cosB）2=0，∠A，∠B都是锐角，则∠C的度数是（　　）

    A. 75° B. 90° C. 105° D. 120°

    C 【解析】【解析】 ∵|sinA﹣|=0，（ ﹣cosB）2=0，∴sinA﹣=0， ﹣cosB=0，∴sinA=， =cosB，∴∠A=45°，∠B=30°，∴∠C=180°﹣∠A﹣∠B=105°．故选C．

    查看答案和解析>>

    科目：初中数学 来源：安徽省宿州市（城西校区） 2017-2018学年九年级第一学期期中测试数学试卷 题型：解答题

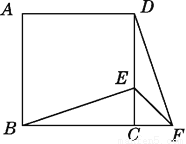
    如图，在正方形ABCD中，E为CD边上一点，F为BC延长线上一点，且CE＝CF.

    求证：△BCE≌△DCF；

    证明见解析 【解析】试题分析：由正方形的性质得出BC＝DC，∠BCE＝∠DCF＝90°，由SAS证明△BCE≌△DCF． 试题解析： 证明：在正方形ABCD中 BC＝DC，∠BCE＝∠DCF＝90°， 在△BCE与△DCF中， ∴△BCE≌△DCF．

    查看答案和解析>>

    科目：初中数学 来源：2017年安徽省中考数学三模试卷 题型：解答题

    市政公司为绿化建设路风景带，计划购买甲乙两种树苗600株，甲种树苗每株50元，乙种树苗每株70元．有关统计表明，甲乙两种树苗的成活率分别为80%和95%．（注：成活率=×100%）．

    （1）若购买树苗的钱不超过40000元，应如何选购甲、乙两种树苗；

    （2）若希望这批树苗的成活率不低于90%，且购买树苗的费用最低，应如何选购甲、乙两种树苗并求出最低费用是多少元．

    （1）选购甲种树苗不少于100株，乙种树苗不超过500株；（2）购买甲种树苗200株，乙种树苗400株时费用最低，最低费用是38000元． 【解析】【试题分析】 （1）根据总费用，列出不等式即可.设选购甲种树苗x株，则选购乙种树苗为（600﹣x）株，根据题意得,50x+70（600﹣x）≤40000，解得x≥100，即选购甲种树苗不少于100株，乙种树苗不超过500株． （2）设...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年北师大版八年级数学下册 期末测评 题型：单选题

    如图所示,在直角△ABC中,∠BAC=90°,AB=8,AC=6,DE是AB边的垂直平分线,垂足为D,交边BC于点E,连接AE,则△ACE的周长为(　)

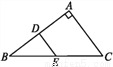
    A. 16 B. 15 C. 14 D. 13

    A 【解析】∵∠BAC=90?，AB=8，AC=6， ∴BC= =10， ∵DE是AB边的垂直平分线， ∴EA=EB， △ACE的周长=AE+EC+AC=BE+EC+AC=BC+AC=16， 故选：D.

    查看答案和解析>>

    同步练习册答案