
将一次函数y=3x﹣1的图象沿y轴向上平移3个单位后,得到的图象对应的函数关系式为____________.
y=3x+2. 【解析】将一次函数y=3x﹣1的图象沿y轴向上平移3个单位后,可得y=3x﹣1+3=3x+2. 故答案为:y=3x+2.科目:初中数学 来源:四川省自贡市2016-2017学年上学期八年级期末统一考试数学试卷 题型:单选题
如图是两个全等三角形,图中的字母表示三角形的边长,则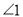 的度数是( )
的度数是( )
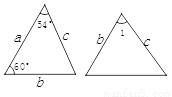
A. 54° B. 60° C. 66° D. 76°
C 【解析】试题解析:根据三角形内角和可得 因为两个全等三角形, 所以 故选C.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市东钱湖九校2017-2018学年八年级上册数学期中联考试卷 题型:填空题
若点M(1-m,2+m)在第四象限内,则m的取值范围是_______.
m<-2 【解析】试题解析:点在第四象限内, 解得: 故答案为:查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏苏州姑苏区第十中学初二上期中试卷数学试卷 题型:解答题
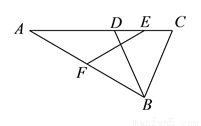
如图,在 中,点
中,点 在边
在边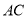 上,
上, 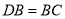 ,
, 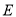 是
是 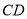 的中点,
的中点, 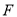 是
是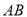 的中点,求证:
的中点,求证: 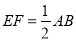 .
.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏苏州姑苏区第十中学初二上期中试卷数学试卷 题型:填空题
如图,已知点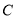 是线段
是线段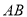 的中点,点
的中点,点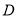 是线段
是线段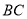 上的定点(不同于端点
上的定点(不同于端点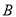 、
、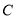 ),过点
),过点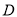 作直线
作直线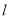 垂直线段
垂直线段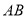 ,若点
,若点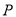 是直线
是直线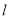 上任意一点,连接
上任意一点,连接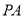 、
、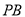 ,则能使
,则能使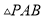 成为等腰三角形的点
成为等腰三角形的点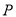 一共有__________个.(填写确切的数字)
一共有__________个.(填写确切的数字)
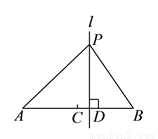
查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏苏州姑苏区第十中学初二上期中试卷数学试卷 题型:单选题
两条直线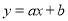 与
与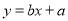 在同一直角坐标系中的图象位置可能是( ).
在同一直角坐标系中的图象位置可能是( ).
A. 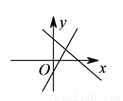 B.
B. 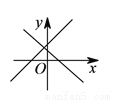
C. 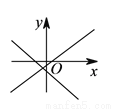 D.
D. 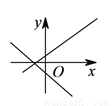
查看答案和解析>>
科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷 题型:解答题
已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
(1)如图1,若该抛物线经过原点O,且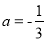 .
.
①求点D的坐标及该抛物线的解析式;
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由;
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余.若符合条件的Q点的个数是3个,请直接写出a的值.
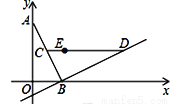
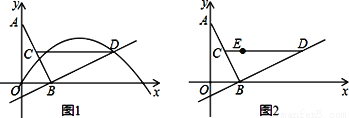
备用图
(1)①D的坐标是(3,1),y=﹣x2+x;②点P(, )或(,﹣);(2)a的值为a=. 【解析】试题分析: (1)①过点D作DF⊥x轴于点F,先通过三角形全等求得D的坐标,把D的坐标和a=﹣,c=0代入y=ax2+bx+c即可求得抛物线的解析式;②先证得CD∥x轴,进而求得要使得∠POB与∠BCD互余,则必须∠POB=∠BAO,设P的坐标为(x,﹣x2+x),分两种情况讨论即可求得;(...查看答案和解析>>
科目:初中数学 来源:江苏省2018届九年级上学期期末模拟数学试卷 题型:单选题
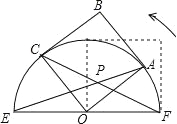
如图,正方形OABC的边长为4,以O为圆心,EF为直径的半圆经过点A,连接AE,CF相交于点P,将正方形OABC从OA与OF重合的位置开始,绕着点O逆时针旋转90°,交点P运动的路径长是( )
A.2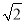 π B.
π B.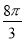 C.4
C.4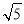 D.6
D.6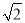
查看答案和解析>>
科目:初中数学 来源:2017年湖南省郴州市中考数学模拟试卷 题型:解答题
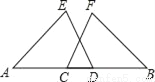
如图,点A、C、D、B四点共线,且AC=BD,∠A=∠B,∠ADE=∠BCF,求证:DE=CF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com