
��ͼ,����˵���������(��)
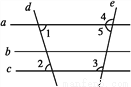
A. ��a��b,b��c,��a��c B. ����1=��2,��a��c
C. ����3=��2,��b��c D. ����3+��5=180��,��a��c
C ���������������������ƽ���ߵ��ж������жϼ��ɣ� �������� A����a��b��b��c����a��c��������ƽ�й�������ȷ�� B������1=��2����a��c���������ڴ�����ȣ���ֱ��ƽ�У���ȷ�� C����3=��2�������ж�b��c������ D������3+��5=180�㣬��a��c������ͬ���ڽǻ�������ֱ��ƽ�У���ȷ�� ��ѡC�� �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ��ɽ��ʡ����� ���꼶����ĩģ����ѧ�Ծ� ���ͣ������
��ͼ��BE��AC��E��CF��AB��F��CF��BE�ཻ�ڵ�D����BD=CD����֤��ADƽ�֡�BAC��
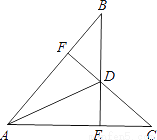
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ��ׯ��������2017-2018ѧ����꼶���ϣ�������ѧ�Ծ� ���ͣ���ѡ��
��ͼ����6���߳�Ϊ1��С�����μ��䲿�ֶԽ��߹��ɵ�ͼ���У���ͼ��A�㵽B��ֻ����ͼ�е��߶��ߣ���ô��A�㵽B�����̾�����߷����У�������
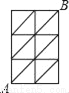
A. 1�� B. 2�� C. 3�� D. 4��
C ��������������������ͼ��ʾ����A�㵽B����߷��������֣����У� �߷�1��2��3�ľ����ǣ� �߷�4��5��6�ľ�����5�� �߷�7��8��9��10�ľ�����. �ߣ����߷�1��2��3�ľ������. ���A�㵽B�����̾�����߷�����3��. ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�ϲ���ĩ���� ���ͣ������
A,B�������20ǧ��,�ס������˶���A��ȥB��,ͼ��l1��l2�ֱ��ʾ�ס�����������·��s(ǧ��)��ʱ��t(Сʱ)֮��Ĺ�ϵ,����˵��:����������1Сʱ;���ҳ���3Сʱ���ϼ�;�ۼ��ٶ���4ǧ��/ʱ;�����ȵ���B��.������ȷ����________.
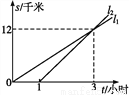
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ�����ѧ���꼶�ϲ���ĩ���� ���ͣ������
��ͼ1�����dz��õ��۵�ʽС��,ͼ2�е���������һ��������ȥһ��С��Բ,���е�Ƭ��������Ե�߿ɿ�������ƽ�е��߶�,ת����Ƭʱ���γ���ͼ2��ʾ�ġ�1���2,���1���2�Ķ�������____��.
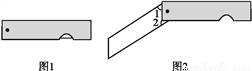
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶12���¿���ѧ�Ծ� ���ͣ������
��ƽ��ֱ������ϵ�У�A�������ǣ�0��6����M�������ǣ�8��0����P������AM��һ�㣬PB��x�ᣬ����ΪB����AP=a��
��1��AM= ��
��2����ͼ����APΪֱ����Բ��Բ��Ϊ��C������C��x�����У���a��ֵ��
��3��D��x����һ�㣬����AD��PD������OAD�ס�BDP����̽�����������ĵ�D�ĸ�����ֱ��д����D�ĸ�������Ӧa��ȡֵ��Χ������˵�����ɣ���
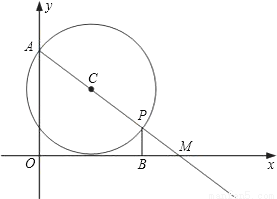
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶12���¿���ѧ�Ծ� ���ͣ������
��1���ⷽ�̣� 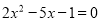 �� ��2��
�� ��2��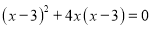
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2018����꼶12���¿���ѧ�Ծ� ���ͣ���ѡ��
������x�ķ���(m��2) x2��2x+1=0����������ȵ�ʵ��������ôm��ȡֵ��Χ�ǣ� ��
A. m<3 B. m<3��m��2�� C. m��3 D. m��3��m��2
B �����������������һԪ���η��̸���������б�ʽ���Ĺ�ϵ����1����������������ȵ�ʵ��������2��������������ȵ�ʵ��������3������û��ʵ������ ������á������ ����Ϊ�� ��m��ȡֵ��Χ���ң��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��ɽ��ʡ�����������2018����꼶���ϣ�������ѧ�Ծ��������棩 ���ͣ���ѡ��
С������̨��Բ���Σ���̨�Ŀ���ABΪ8m����̨�������C����AB�ľ���CDΪ2m������̨����Բ�İ뾶Ϊ��������
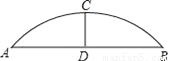
A. 4m B. 5m C. 6m D. 7m
B ����������ͼ����Բ��ΪO�㣬����OA��OD�� ������ɵã���O��C��D��ͬһֱ���ϣ���OC��AB�� ��DΪAB���е㣬��AD=BD=AB=4��m���� ��Բ�뾶Ϊr������OD=OC��CD=��r��2��m�� ��Rt��AOD�У�OA2=AD2+OD2����r2=42+��r��2��2�� ��ã�r=5�� ����̨����Բ�İ뾶Ϊ5m�� ��ѡB�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com