
若点A(2,-3)、B(4,3)、C(5,a)在同一条直线上,则a的值是( )
A. 6或-6 B. 6 C. -6 D. 6或3
B 【解析】设一次函数的解析式为y=kx+b,把A(2,?3)、B(4,3)、C(5,a)代入得 ,解得. a的值是6.故选B.科目:初中数学 来源:江苏省徐州市丰县2018届九年级上学期第二次月考数学试卷 题型:单选题
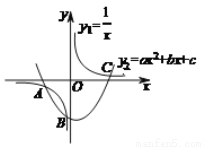
如图,反比例函数y1=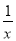 与二次函数y2=ax2+bx+c图象相交于A、B、C三个点,则函数y=ax2+bx-
与二次函数y2=ax2+bx+c图象相交于A、B、C三个点,则函数y=ax2+bx- +c的图象与X轴交点的个数是( )
+c的图象与X轴交点的个数是( )
A. 3 B. 2 C. 1 D. 0
A 【解析】当时,得=ax²+bx+c,即ax²+bx?+c=0, ∵方程的解即反比例函数与二次函数=ax²+bx+c图象交点的横坐标, ∵反比例函数=与二次函数=ax²+bx+c图象相交于A. B. C三个点, ∴函数y=ax²+bx?+c的图象与x轴交点即是ax2+bx?1x+c=0的解, ∴函数y=ax²+bx?+c的图象与x轴交点的个数是3个, 故选A....查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西省七年级(下)第二次测验数学试卷 题型:填空题
如图,点C、D是线段AB上的两点,若AC=4,CD=5,DB=3,则图中所有线段的和是_____.

查看答案和解析>>
科目:初中数学 来源:江苏省徐州市丰县2017-2018学年八年级上学期第二次月考数学试卷 题型:解答题
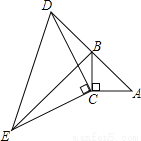
如图,在△ABC中,∠ACB=90°,AC=BC,延长AB至点D,使DB=AB,连接CD,以CD为直角边作等腰直角三角形CDE,其中∠DCE=90°,连接BE.
(1)求证:△ACD≌△BCE;
(2)若AC=3,求BE的长度.
查看答案和解析>>
科目:初中数学 来源:江苏省徐州市丰县2017-2018学年八年级上学期第二次月考数学试卷 题型:单选题
如图,△ABC中,  ,E是边AB上一点,
,E是边AB上一点, 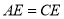 ,过E作
,过E作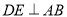 交BC于D,连结AD交CE于F,若
交BC于D,连结AD交CE于F,若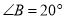 ,则
,则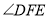 的大小是( )
的大小是( )
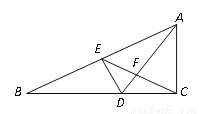
A. 40° B. 50° C. 60° D. 70°
C 【解析】∵∠ACB=90°, ∠B=20°, ∴∠BAC=70°, ∵AE=CE, ∴∠BAC=∠ACE=70°, ∴∠AEC=180°-70°-70°=40°,∵, ∴∠ACB=90°, ∴∠ECB=20°, ∴∠B=∠ECA=20°, ∴BE=CE=AE, ∴ED垂直平分AB, ∴AD=AB, ∴∠B=∠BAD=20°, ∵∠DFE=∠BAD+AEC, ∴∠DFE=20°+40°=6...查看答案和解析>>
科目:初中数学 来源:安徽省16-17学年度第一学期七年级数学期末考试卷 题型:解答题
已知,如图,B,C两点把线段AD分成2∶5∶3三部分,M为AD的中点,BM=6 cm,求CM和AD的长.
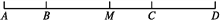
查看答案和解析>>
科目:初中数学 来源:安徽省16-17学年度第一学期七年级数学期末考试卷 题型:填空题
请写出一个所含字母只有x、y,且二次项系数和常数项都是-5的三次三项式:________________________.
答案不唯一,如x3―5xy―5 【解析】利用多项式的项数和次数的定义写出一个满足条件的多项式即可. 【解析】 所有字母只有x,y,且二次项系数和常数项都是-5的三次三项式可为x3-5xy-5. 故答案为:x3-5xy-5.查看答案和解析>>
科目:初中数学 来源:山西农业大学附属中学2017-2018学年八年级上学期第三次月考数学试卷 题型:解答题
已知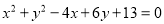 ,求
,求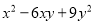 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:黑龙江省哈尔滨市香坊区2017年中考数学二模试卷(解析版) 题型:单选题
已知点A(2,y1)、B(4,y2)都在反比例函数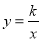 (k<0)的图象上,则y1、y2的大小关系为( )
(k<0)的图象上,则y1、y2的大小关系为( )
A. y1>y2 B. y1<y2 C. y1=y2 D. 无法确定
B 【解析】试题分析:∵当k<0时,y=在每个象限内,y随x的增大而增大,∴y1<y2,故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com