练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，反比例函数y1=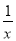与二次函数y2=ax2+bx+c图象相交于A、B、C三个点，则函数y=ax2+bx-+c的图象与X轴交点的个数是（ ）

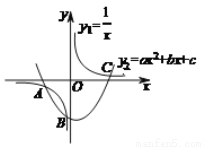
    A. 3 B. 2 C. 1 D. 0

    A 【解析】当时,得=ax²+bx+c,即ax²+bx?+c=0， ∵方程的解即反比例函数与二次函数=ax²+bx+c图象交点的横坐标， ∵反比例函数=与二次函数=ax²+bx+c图象相交于A. B. C三个点， ∴函数y=ax²+bx?+c的图象与x轴交点即是ax2+bx?1x+c=0的解， ∴函数y=ax²+bx?+c的图象与x轴交点的个数是3个， 故选A....
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2016-2017学年内蒙古乌海市七年级（下）期末数学试卷 题型：填空题

    =_____．

    1 【解析】试题解析：原式 故答案为：1.

    查看答案和解析>>

    科目：初中数学 来源：2017年湖北省黄冈市中考数学三模试卷 题型：解答题

    已知：如图，在菱形ABCD中，E、F分别是BC、CD的中点．

    （1）求证：△ABE≌△ADF；

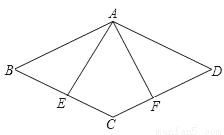
    （2）过点C作CG∥EA交AF于H，交AD于G，若∠BAE=25°，∠BCD=130°，求∠AHC的度数．

    (1)证明见解析；（2）100°. 【解析】试题分析：根据菱形的性质可得AB=AD，∠B=∠D，BE=DF，利用SAS判定△ABE≌△ADF；由△ABE≌△ADF可得∠BAE=∠DAF=25°，从而可推出∠EAF的度数，根据平行线的性质可得到∠AHC的度数． 试题分析：（1）证明：菱形ABCD中，AB=BC=CD=AD，∠B=∠D， ∵E、F分别是BC、CD的中点， ∴BE...

    查看答案和解析>>

    科目：初中数学 来源：江苏省徐州市丰县2018届九年级上学期第二次月考数学试卷 题型：解答题

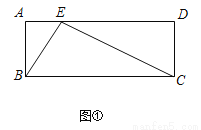
    在矩形ABCD中，AB＝4，BC＝10，E是直线AD上任意一点（不与点A重合），点A关于直线BE的对称点为A′，AA′所在直线与直线BC交于点F．

    （1）如图①，当点E在线段AD上时，①若△ABE ∽△DEC，求AE的长；

    ②设AE＝x，BF＝y，求y与x的函数表达式．

    （2）线段DA′的取值范围是 ．

    （1）①2或8；②y=；（2）≤DA′≤． 【解析】分析：（1）①设AE=x,再根据对应边成比例可得到关于x的一元二次方程，求解即可；②由，推出 ，由对应线段成比例得到关于x, y的方程，变形即可；（2）对称轴和对称点连线的交点在以线段AB为直径的圆上，D最短时 ， 在对角线BD. 本题解析： （）①设，则， ∵， ∴， 即， ∴， ∴， ， ...

    查看答案和解析>>

    科目：初中数学 来源：江苏省徐州市丰县2018届九年级上学期第二次月考数学试卷 题型：填空题

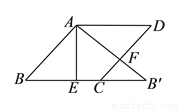
    如图，在边长为2的菱形ABCD中，∠B=45°，AE为BC边上的高，将△ABE沿AE所在直线翻折得△AB＇E，AB＇与CD边交于点F，则B＇F的长度为_______

    【解析】∵在边长为2的菱形ABCD中,∠B=45°，AE为BC边上的高， ∴AE=,由折叠易得△ABB′为等腰直角三角形， ∴S△ABB′=BA?AB′=2,S△ABE=1， ∴CB′=2BE?BC=2?2， ∵AB∥CD， ∴∠FCB′=∠B=45?， 又由折叠的性质知,∠B′=∠B=45?， ∴CF=FB′=2?. 故答案为：2?.

    查看答案和解析>>

    科目：初中数学 来源：2017广东省深圳市中考数学模拟试卷（三） 题型：解答题

    某汽车厂计划半年内每月生产汽车20辆，由于另有任务，每月工作人数不一定相等，实际每月生产量与计划量相比情况如表（增加为正，减少为负）

    月份

    一

    二

    三

    四

    五

    六

    增减（辆）

    +3

    ﹣2

    ﹣1

    +4

    +2

    ﹣5

    ①生产量最多的一月比生产量最少的一月多生产多少辆？

    ②半年内总产量是多少？比计划增加了还是减少了，增加或减少多少？

    （1）9辆；（2）半年内总产量是121辆，比计划增加了1辆． 【解析】试题分析：①利用表中的最大数减去最小的数即可； ②半年内的计划总产量是20×6=120辆，然后求得六个月中的增减的总和即可判断． 试题解析：①生产量最多的一月比生产量最少的一月多生产4﹣（﹣5）=9（辆）； ②总产量是：20×6+（3﹣2﹣1+4+2﹣5）=121（辆）， 3﹣2﹣1+4+2﹣5=1...

    查看答案和解析>>

    科目：初中数学 来源：2017广东省深圳市中考数学模拟试卷（三） 题型：填空题

    如果a，b两数互为相反数，则a﹣3+b=　 　．

    -3. 【解析】试题解析：∵a，b两数互为相反数， ∴a+b=0， ∴a-3+b=a+b-3=0-3=-3． 故答案为：-3．

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年陕西省七年级（下）第二次测验数学试卷 题型：解答题

    结合数轴与绝对值的知识回答下列问题：

    （1）探究归纳：①数轴上表示5和2的两点之间的距离是　 　；

    ②数轴上表示﹣2和﹣6的两点之间的距离是　 　；

    ③数轴上表示﹣4和3的两点之间的距离是　 　；

    一般地，数轴上表示数m和数m的两点之间的距离等于|m﹣n|．

    （2）应用：

    ①若数轴上表示数a的点位于﹣4与3之间，则|a+4|+|a﹣3|的值为　 　；

    ②当a=　 　，|a+4|+|a﹣1|+|a﹣3|的值最小，最小值是　 　．

    （1）①3，②4，③7；（2）①7，②1，7 【解析】试题分析：（1）根据两点间的距离公式，可得答案； （2）①根据两点间的距离公式，可得答案； ②根据线段上的点到线段两端点的距离的和最小，分类讨论可求得答案； 试题解析：（1）由题意可得， ①数轴上表示5和2的两点之间的距离是：5﹣2=3， ②数轴上表示﹣2和﹣6的两点之间的距离是：（﹣2）﹣（﹣6）=4， ③数...

    查看答案和解析>>

    科目：初中数学 来源：江苏省徐州市丰县2017-2018学年八年级上学期第二次月考数学试卷 题型：单选题

    若点A（2，-3）、B(4，3)、C(5，a)在同一条直线上，则a的值是( )

    A. 6或-6 B. 6 C. -6 D. 6或3

    B 【解析】设一次函数的解析式为y=kx+b,把A(2,?3)、B(4,3)、C(5,a)代入得 ，解得. a的值是6.故选B.

    查看答案和解析>>

    同步练习册答案