
��һ�������������ڽǵĶ���֮��Ϊ1��2��3��������������е����ĽǶ��� ��
90�� �������� �����������֪�����������ڽǵĶ���֮�ȣ�������һ��Ϊk�����������ε��ڽǺ͵���180���з����������ڽǵĶ������Ӷ�ȷ�������ε����ǵĶ����� �������� �������ڽǵĶ����ֱ�Ϊk��2k��3k�� ��k+2k+3k=180�㣬 ���k=30�㣬 ��2k=60�㣬3k=90�㣬 ������������Ľǵ���90�㣮 �ʴ�Ϊ��90�㣮 ����ѧ����ϵ�д�
����ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017�����ʡ�人���п���ѧģ���Ծ��� ���ͣ���ѡ��
�����A��B��C��D����Ӧ����Ϊa��b��c��d����a��b��c��d�Ĵ�С��ϵ�ǣ�������
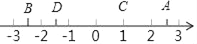
A. a��c��d��b B. b��d��a��c C. b��d��c��a D. d��b��c��a
C ���������������ұߵĵ��ʾ����������ߵĵ�����ʾ����������b��d��c��a. ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���Ĵ�ʡ�ϳ���Ӫɽ�س��϶�С2017-2018ѧ����ѧ�ھ��꼶��ѧ��ĩ��������Ծ� ���ͣ������
��ƽ��ֱ������ϵ�У���������C1��y=x2�Ƶ㣨1��0����ת180��õ�������C2������������C1��C2��λ�ک�2��x��2��Χ�ڵIJ���Ϊͼ��C3����һ�κ���y=kx+k��1��k��0����ͼ����ͼ��C3���������㣬��k�ķ�Χ�ǣ�__��
��2+2��k�ܻ��k�ܩ�4+6��k��15 �������������������ͼ,������ͼ��Ľ���ʽΪ ͼ����ͼ����������֮����ϵIJ���ͼ��. ��,��A(2,4),B(?2,?16),D(2,0). ��Ϊһ�κ���y=kx+k?1(k>0)��ͼ����ͼ������������ ��ֱ�߾�����Aʱ,��������,4=2k+k?1,��� �ڵ�ֱ��������������ʱ,�� ��ȥy�õ� �ߡ�=0�� ��û� ...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʮ����2017-2018ѧ��������ĩ���꼶��ѧ�Ծ� ���ͣ������
(10��)��֪��ABC�ǵȱ������Σ���D��ֱ��BC��һ�㣬��ADΪһ����AD���Ҳ����ȱߡ�ADE.
(1)��ͼ�٣���D���߶�BC���ƶ�ʱ��ֱ��д����BAD�͡�CAE�Ĵ�С��ϵ��
(2)��ͼ�ڣ���D���߶�BC���ӳ������ƶ�ʱ�������DCE�Ĵ�С�Ƿ����仯����������������С�����仯����˵�����ɣ�
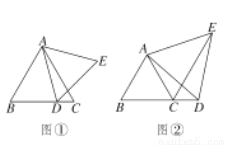
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʮ����2017-2018ѧ��������ĩ���꼶��ѧ�Ծ� ���ͣ������
���㣺
��1������a2��3•4a ��2��2x��x+1��+��x+1��2��
(1)-4a7; (2) 3x2+4x+1�� ���������������:��1�������ݵij˷���ͬ�����ݵij˷����м��㼴�ɣ� ��2�����ݵ���ʽ���Զ���ʽ�Լ���ȫƽ����ʽ���м��㼴�ɣ� �������� ��1��ԭʽ=��a6•4a =��4a7�� ��2��ԭʽ=2x2+2x+x2+2x+1 =3x2+4x+1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��������ʮ����2017-2018ѧ��������ĩ���꼶��ѧ�Ծ� ���ͣ���ѡ��
���д����ҵ���������ʽ�ֽ����( )
A. 2a2��2a+1=2a��a��1��+1 B. ��x��y����x+y��=x2��y2
C. 9x2��6x+1=��3x��1��2 D. x2+y2=��x��y��2+2xy
C ��������A.û��һ������ʽת���ɼ�����ʽ������ʽ����A���� B������ʽ�ij˷�����B���� C����һ������ʽת���ɼ�����ʽ������ʽ����C��ȷ�� D��û��һ������ʽת���ɼ�����ʽ������ʽ����D���� ��ѡ��C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꼪��ʡ�������п���ѧģ���Ծ� ���ͣ������
��ͼ����ƽ��ֱ������ϵ�У�������y=x2+bx+c��x�ύ�ڵ�A����1��0����B��3��0������y�ύ�ڵ�C����ֱ��BC����P����������һ�����㣨��P�����B��C�غϣ�������PB��PC����PB��PCΪ����?CPBD����?CPBD�����ΪS����P�ĺ�����Ϊm��
��1���������߶�Ӧ�ĺ�������ʽ��
��2������P�ڵ������ޣ���?CPBD������������x����ʱ�����P�����ꣻ
��3����S��m֮��ĺ�����ϵʽ��
��4����x�Ὣ?CPBD������ֳ�1��7������ʱ��ֱ��д��m��ֵ��
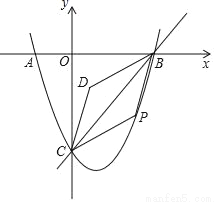
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꼪��ʡ�������п���ѧģ���Ծ� ���ͣ���ѡ��
��ͼ���ı���ABCD�ǡ�O���ڽ��ı��Σ�����B=80�㣬���ADC�Ķ����ǣ�������
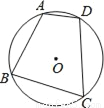
A. 60�� B. 80�� C. 90�� D. 100��
D �����������ı���ABCD�ǡ�O���ڽ��ı��Σ� ���ADC=180��-��B=180��-80��=100��. ��ѡD.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017�꺣��ʡ�������п���ѧ�����Ծ������� ���ͣ������
ij�����̳�����A��B�����ͺż����������ּ������Ľ����۸�ֱ�Ϊÿ̨30Ԫ��40Ԫ���̳�����5̨A�ͺź�1̨B�ͺż��������ɻ�����76Ԫ������6̨A�ͺź�3̨B�ͺż��������ɻ�����120Ԫ�����̳�����A��B�����ͺż����������ۼ۸�ֱ��Ƕ���Ԫ��������=���ۼ۸����۸�
A���ͺż����������ۼ۸���42Ԫ��B���ͺż����������ۼ۸���56Ԫ�� �������������������A���ͺż����������ۼ۸���xԪ��B���ͺż����������ۼ۸���yԪ����������ɵ�����ϵ����5̨A�ͺź�1̨B�ͺż��������ɻ�����76Ԫ��������6̨A�ͺź�3̨B�ͺż��������ɻ�����120Ԫ�����ݵ�����ϵ�г������飬�ٽ⼴��. ��������� ��A���ͺż����������ۼ۸���xԪ��B���ͺż����������ۼ۸�...�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com